Volumen (Física)
El volumen en física es la extensión de un cuerpo en sus tres dimensiones, la cual toma en cuenta el ancho, longitud y altura o profundidad del mismo.
Podemos representar el volumen solamente con un valor y una unidad; por ello, es una magnitud escalar. Es decir, un cubo de 4 metros cúbicos siempre tendrá el mismo valor sin importar el punto de referencia o el observador que mida el cubo.
En otras palabras, el volumen es la medida del espacio que ocupa un elemento. Los seres vivos, muebles, vehículos, celulares, bebidas, todo ocupa un espacio, y por extensión, presenta volumen.
En el Sistema Internacional de Unidades, el volumen se mide en metros cúbicos (m3). Hay otras unidades que se suelen emplear según la cantidad o cuerpo a medir, como:
- el litro o decímetro cúbico (dm3), que equivale a 0,001 m3;
- el centímetro cúbico, que equivale a 0,000001 m3;
- el centilitro, que equivale a 0,01 litros;
- o el mililitro, que equivale a 0,001 litros.
Fórmulas para sacar el volumen
El cálculo del volumen varía según la forma que tiene el cuerpo o sustancia a medir. A continuación compartimos fórmulas para determinar el volumen de diferentes figuras geométricas, como el cubo, la esfera, la pirámide o los prismas.
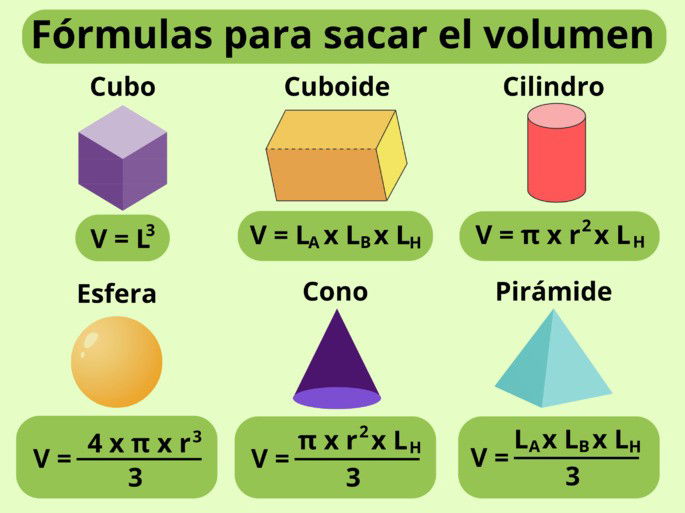
- Volumen de un cubo = L3, en el que L corresponde a la longitud de uno de los lados del cubo. Recuerda que todos los lados de un cubo miden igual.
- Volumen de un cuboide = LA x LB x LH, en el que LA es el ancho, LB el largo, y LH la altura de la figura. También se conoce como paralelepípedo o prisma cuadrangular.
- Volumen de un cilindro = π x r2 x LH, en el que r equivale al radio de la base del cilindro, y LH a su altura.
- Volumen de una esfera = (4 x π x r3) / 3, en el que r corresponde al radio de la esfera.
- Volumen de un cono = (π x r2 x LH) / 3, en el que r corresponde al radio del círculo en la base del cono, y LH a la altura del cono desde la base.
- Volumen de una pirámide = (LA x LB x LH) / 3, en el que LA es el ancho de la base, LB el largo, y LH la altura de la pirámide desde la base.
Pongamos por ejemplo un cubo que sea de 5 centímetros de longitud. Si empleamos la fórmula del cubo, veremos que posee un volumen de 125 cm3:
Otro ejemplo es una esfera cuyo radio mide 12 cm. Al servirnos de la fórmula para la esfera, obtenemos que el volumen es 7238 cm3:
¿Qué hay de un cono de 2 metros de altura y un radio de 1,2 metros? Utilicemos la fórmula correspondiente:
En este caso, el volumen del cono es 3,016 m3.
Cálculo del volumen de los prismas
Para calcular el volumen de los prismas distintos al cuadrangular, conviene primero calcular el área de la base, A. Una vez determinada el área, el volumen de todos los prismas se obtiene con la ecuación A x LH, en el que LH es la altura del prisma.
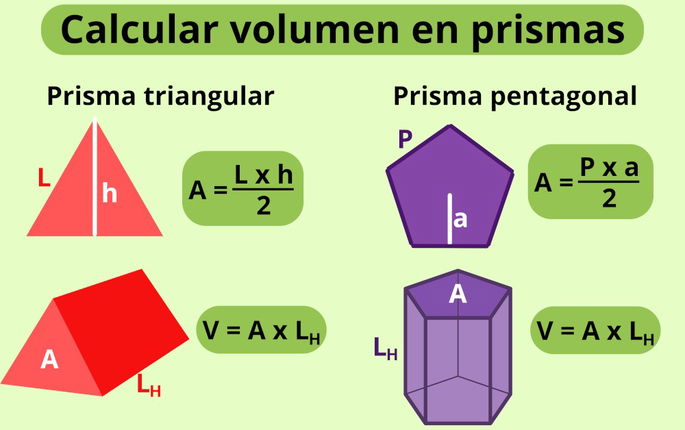
Por ejemplo, para obtener el volumen de un prisma de base triangular y otro pentagonal, primero calculamos sus áreas:
- Área de la base triangular = (L x h) / 2, en el que L es la longitud de uno de los lados del triángulo equilátero, y h la altura del triángulo desde el centro de un lado hasta el vértice opuesto.
- Área de la base pentagonal = (P x a) / 2, en el que P es el perímetro de la base, y a la apotema, que marca la distancia entre el centro de uno de los lados y el centro de la base.
Calculada el área de la base correspondiente, solo te queda multiplicar dicho valor por la altura del prisma. Con ello, ¡obtendrás el volumen!
Para ilustrar esto, supongamos que tenemos un prisma triangular con los siguientes datos:
- L = 6 cm, que corresponde a la longitud de cada lado del triángulo.
- h = 5,2 cm, que corresponde a la altura de la base triangular.
- LH = 8 cm, que corresponde a la altura del prisma.
Empleamos las fórmulas correspondientes, y obtenemos:
Como segundo ejemplo, imaginemos que hay un prisma hexagonal con los siguientes datos:
- P = 18 cm, que corresponde al perímetro de la base hexagonal.
- a = 2,6 cm, que corresponde a la apotema de la base hexagonal.
- LH = 10 cm, que corresponde a la altura del prisma.
Para calcular el volumen del prisma hexagonal, las fórmulas a utilizar son las mismas a la de un prisma pentagonal:
Relación entre volumen, masa y densidad
La densidad es una propiedad física, característica de cada cuerpo, que relaciona la cantidad de masa de una sustancia por unidad de volumen. Si en esta relación de variables despejamos el volumen, obtenemos la siguiente fórmula:
En el que:
- V es el volumen;
- m es la masa; y
- ρ es la densidad.
Gracias a esta relación entre variables, podemos calcular el volumen si conocemos los valores de la masa y densidad, incluso si el cuerpo posee una forma geométrica irregular.
Imaginemos que tenemos una mesa de madera de 40 kg que posee una densidad de 550 kg/m3. Como tenemos la masa y la densidad, podemos servirnos de la fórmula:
Por lo tanto, esta relación de variables es útil si queremos saber el volumen de una sustancia con forma irregular, a diferencia de un cubo, cilindro, esfera o similares.
Ejemplos del cálculo de volumen
Aquí presentamos unos ejercicios que te ayudarán a asimilar lo aprendido en este artículo.
Ejercicio 1
Tenemos un cuboide o prisma cuadrangular con las siguientes dimensiones:
- 32 centímetros de altura
- 14 centímetros de ancho
- 8 centímetros de largo
¿Cuál es el volumen del cuboide?
Ejercicio 2
Un cilindro de 25 centímetros de alto posee una base con un diámetro de 18 centímetros. ¿Qué volumen tiene?
Ejercicio 3
Se nos muestra una pirámide de base cuadrada que mide 15 metros de altura y 27 metros de ancho. ¿Cuál es el volumen de la pirámide?
Ejercicio 4
Tenemos un prisma pentagonal con las siguientes dimensiones:
- 18 centímetros de altura del prisma
- 5 centímetros de cada lado de la base pentagonal
- 3,44 centímetros la apotema de la base pentagonal
Vea también:
Cómo citar: Rhoton, Stephen (29/04/2025). "Volumen (Física)". En: Significados.com. Disponible en: https://www.significados.com/volumen-fisica/ Consultado: