Trigonometría
La trigonometría es un área de las matemáticas que estudia las relaciones que tienen cada uno de los elementos de un triángulo. En general, el triángulo que se estudia es el triángulo rectángulo, o sea, aquel en que uno de sus lados mide 90º.
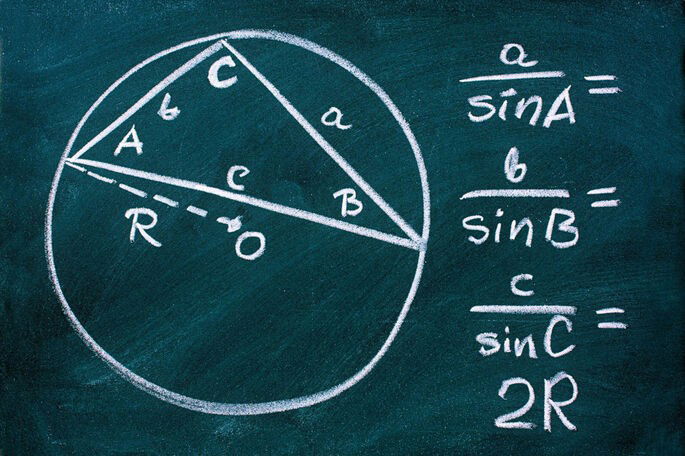
La trigonometría ya existía hace más de 3000 años, cuando los babilonios y los egipcios usaban los ángulos de los triángulos para construir pirámides y otras estructuras arquitectónicas complejas hasta para la tecnología moderna.
Las estrellas del cielo fueron objeto de estudio en la trigonometría, pues a partir de ellas se crearon mapas estelares para calcular rutas, predecir fenómenos meteorológicos y espaciales, fabricar relojes y calendarios, etc. Por esta razón, la trigonometría está fuertemente ligada con la astronomía.
La función seno de la trigonometría ya era trabajada por los astrónomos árabes del siglo VIII. En el plazo de los dos siguientes siglos descubrieron 6 funciones y demostraron los teoremas fundamentales de la trigonometría.
Con el paso del tiempo, la trigonometría se convirtió en una rama independiente de la matemática cuando la corriente llega a Europa, separándola de la astronomía. Actualmente, la trigonometría se emplea en muchos campos de ciencias e ingeniería, debido a que nos permite realizar cálculos muy precisos.
La trigonometría proviene de la composición de la palabra griega trigonos, que significa triángulo, y de la palabra metros, que significa medida o medición.
Elementos y conceptos claves en la trigonometría
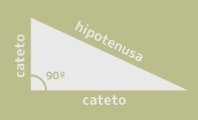
Los elementos principales a destacar en la trigonometría son los triángulos y sus componentes, especialmente los de un triángulo rectángulo. Los ángulos y los lados compuestos por catetos e hipotenusa, así como las relaciones que hay entre ellos, son el pilar central de la trigonometría.
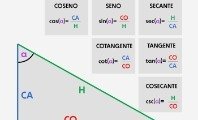
Por ello, en trigonometría se habla de las razones trigonométricas. Las 3 razones básicas que se deben considerar para entender la trigonometría son: el seno de x (senx), el coseno de x (cosx) y la tangente de x (tanx o tgx).
En la siguiente imagen ejemplificaremos el ángulo como alfa (α):
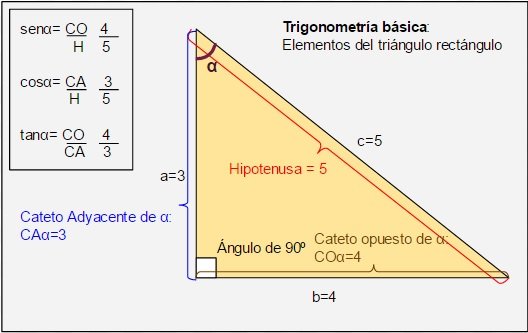
Tomando como referencia la figura de la imagen, podemos establecer las siguientes fórmulas básicas de la trigonometría:
El seno de un ángulo
senα = cateto opuesto / hipotenusa = 4 / 5
El coseno de un ángulo
cosα = cateto adyacente / hipotenusa = 3 / 5
La tangente de un ángulo
tanα = cateto opuesto / cateto adyacente = 4 / 3
Además de estas razones trigonométricas básicas, existen las recíprocas de cada una: la secante, la cosecante y la cotangente. Otros conceptos relacionados son las funciones inversas de todas estas razones, como el arcoseno o el arcotangente.
A partir de la trigonometría se emplean las funciones trigonométricas, que son aquellas funciones cuya variable independiente es un ángulo. Este tipo de funciones son periódicas, es decir, si las dibujamos en el plano cartesiano, veremos que describen un patrón que se repite.
Relacionado con lo anterior, en trigonometría se establecen las identidades trigonométricas, que son ecuaciones que relacionan las diferentes funciones trigonométricas.
Respecto al cálculo y representación de los ángulos, las unidades empleadas varían según el campo de ciencias o ingeniería. Las unidades más utilizadas son los grados sexagesimales, que surge de la división de una circunferencia en 360 partes iguales, y radianes, que relaciona la longitud del arco de la circunferencia con la longitud de su radio.
Finalmente, como el estudio de triángulos rectángulos forma parte de la trigonometría, la aplicación del teorema de Pitágoras es clave de cara a determinar los lados de un triángulo.
Vea también Triángulo rectángulo.
Aplicaciones de la trigonometría
La trigonometría tiene numerosas aplicaciones en distintos campos y sectores, más allá de las matemáticas puras y la geometría.
Por ejemplo, la trigonometría se emplea bastante en la astronomía para calcular las distancias entre dos cuerpos celestes o el tamaño de los mismos. Gracias a ella, podemos conocer la distancia entre la Tierra y la Luna o el Sol en cualquier momento del año.
Además, la trigonometría ha servido y sigue sirviendo para la navegación náutica y la cartografía. Por un lado, el estudio de las estrellas y el cálculo de sus posiciones sirve para orientarnos, asegurar que vamos en la dirección correcta. Por el otro lado, es útil para determinar la distancia entre distintos puntos y elaborar mapas detallados.
En la arquitectura e ingeniería civil, la trigonometría es vital en la elaboración de planos y en las construcciones de todo tipo, ya sean casas, edificios de oficina o industriales, puentes, carreteras, etc. Una gran razón es que la trigonometría nos permite hacer cálculos muy precisos.
En la física se utiliza en el cálculo de trayectoria de objetos, tales como la de un cohete o la de un asteroide que atraviesa el sistema solar. También es común la presencia de la trigonometría en el estudio y cálculo de ondas o cualquier fenómeno ondulatorio.
Por último, la trigonometría sirve muchísimo en todos los campos de ingeniería, como por ejemplo en el diseño y fabricación de piezas industriales o la programación de máquinas.
Vea también Matemáticas y Triángulo rectángulo.
Cómo citar: Rhoton, Stephen (25/07/2025). "Trigonometría". En: Significados.com. Disponible en: https://www.significados.com/trigonometria/ Consultado: