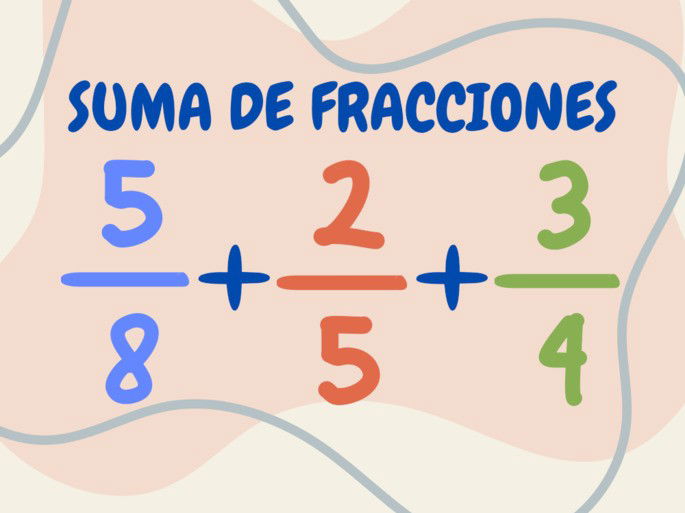
Suma de fracciones
La suma de fracciones es una operación aritmética de adición realizada entre dos números fraccionarios o más. Los números fraccionarios son aquellos que expresan las partes de un entero, y se componen de un numerador y un denominador.
Para que las fracciones se puedan sumar, es necesario que todas tengan el mismo denominador. Existen varios métodos para lograr este cometido y resolver las sumas de fracciones. En general, nos servimos del método de la mariposa o el mínimo común múltiplo. ¡Ambos son correctos!
No obstante, la manera de resolver estas sumas variará según el denominador sea igual o diferente.
Suma de fracciones con igual denominador
Cuando los denominadores de todas las fracciones son iguales, la operación es bastante sencilla. En este caso, solo debemos sumar los numeradores y mantener el mismo denominador.
Por ejemplo, si tenemos la siguiente suma de fracciones:
El denominador de las tres fracciones coincide, 5. Esto significa que, para resolver la suma de fracciones, solo nos queda sumar los numeradores:
Suma de fracciones con diferente denominador
Cuando los denominadores de las fracciones no coinciden, el proceso es menos directo. Primero hemos de seguir unos pasos para lograr que el denominador sea común en todas las fracciones. Luego, se suman los numeradores.
Suma de dos fracciones con diferente denominador
En las sumas de dos fracciones con diferente denominador, se suele emplear el método de la mariposa. Ilustremos esto con un ejemplo.
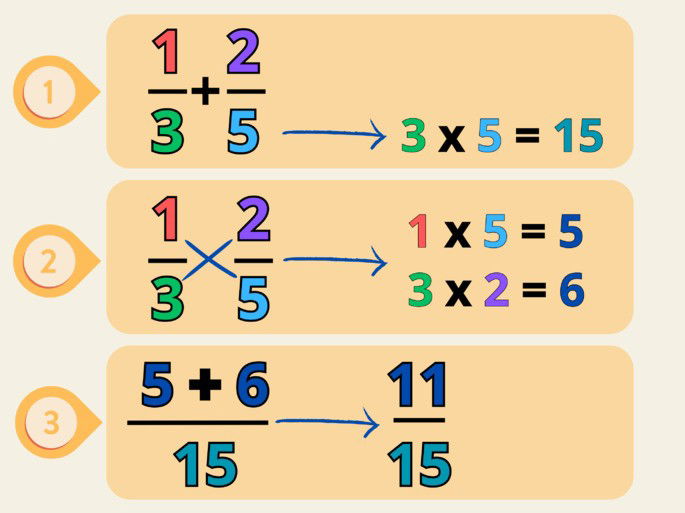
Imaginemos que tenemos la siguiente suma de fracciones:
Primero hemos de hallar el denominador resultante de esta operación. Para ello, simplemente multiplicamos los denominadores:
Ahora, para conocer los nuevos numeradores de cada fracción, nos servimos del método de la mariposa. Este método nos dice que hemos de multiplicar en cruz el numerador de la primera fracción por el numerador de la segunda fracción. Luego, hay que multiplicar el numerador de la segunda fracción por el denominador de la primera.
Es decir:
Finalmente, se suman los nuevos numeradores, y obtenemos así el resultado de la suma de fracciones:
Suma de tres fracciones o más con diferente denominador
Cuando se suman tres fracciones o más, solemos servirnos del mínimo común múltiplo o mcm para resolver la operación. Pongamos el siguiente ejemplo:
Primero hemos de hallar el mínimo común múltiplo de los denominadores para conocer el denominador resultante de la operación. En este caso, es:
A continuación, para encontrar los nuevos numeradores, se divide el mínimo común múltiplo por el denominador de cada fracción, y luego se multiplica por el numerador de dichas fracciones.
Es decir:
Ahora que hemos hallado los nuevos numeradores y denominadores, procedemos con la suma:
Suma de fracciones mixtas
Las sumas de fracciones mixtas requieren un paso más para resolverlas. En general, la mejor forma es separar las partes enteras de las fraccionarias en este tipo de fracciones, y realizar las sumas por separado.

Por ejemplo, si tenemos la siguiente suma de fracciones mixtas:
Primero separamos los números enteros de los fraccionarios y los sumamos:
Luego, realizamos la suma de fracciones sin la parte entera, sirviéndonos del método de la mariposa o el mcm. A continuación, solo te queda juntar el número entero con la fracción final.
En este caso, sería:
Ejemplos de sumas de fracciones
A continuación, mostramos unos ejercicios de sumas de dos o más fracciones, incluyendo dos casos que contienen fracciones mixtas.
Ejercicio 1
Resuelve la siguiente suma de dos fracciones:
Ejercicio 2
Resuelve esta suma de dos fracciones mixtas:
Ejercicio 3
Resuelve esta suma de estas tres fracciones:
Ejercicio 4
Resuelve la siguiente suma de tres fracciones:
Ejercicio 5
Resuelve esta suma de tres fracciones mixtas:
Ejercicio 6
Resuelve la siguiente suma de cuatro fracciones:
Vea también:
Cómo citar: Rhoton, Stephen (31/03/2025). "Suma de fracciones". En: Significados.com. Disponible en: https://www.significados.com/suma-de-fracciones/ Consultado: