Tipos de probabilidad
La probabilidad en estadística y matemáticas es el número de posibilidades que existen de que ocurra un evento particular. Esta cifra es el resultado de un cálculo numérico que se realiza mediante fórmulas diferentes, dependiendo del tipo de probabilidad que se esté estudiando.
Por ejemplo, si lanzamos un dado de seis cifras, podemos decir que existe 1 posibilidad entre 6 de que salga el número 5. Pero también podríamos decir que existe un 16,6% de posibilidades de que saquemos un 5, resultado de dividir 1 entre 6 y multiplicarlo por 100 para obtener el porcentaje. Esto es lo que llamamos como probabilidad simple.
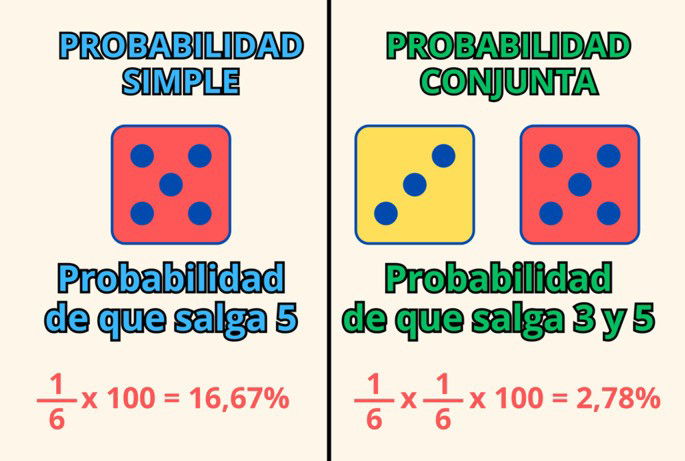
Sin embargo, para calcular la probabilidad de que sucedan dos eventos diferentes simultáneamente, debemos servirnos de otro tipo de probabilidad. Concretamente, la probabilidad conjunta. O si queremos estudiar la probabilidad de que un evento suceda después de darse otro evento, emplearemos la probabilidad condicional.
A continuación mostramos los tipos principales de probabilidad que hay en la estadística o matemáticas, con fórmulas y ejemplos:
- Probabilidad clásica o simple
- Probabilidad frecuencial
- Probabilidad subjetiva
- Probabilidad conjunta
- Probabilidad marginal
- Probabilidad condicional
- Probabilidad bayesiana
- Probabilidad geométrica
Probabilidad clásica o simple
La probabilidad clásica o simple es el resultado de dividir el número de casos favorables (número de veces en que se produce un evento) entre el número total de casos posibles. Se trata de un cálculo teórico, basado en la lógica matemática y no en la experiencia.
Por ello, se ajusta muy bien a eventos o situaciones cuyo número de posibilidades es fácilmente calculable, como la tirada de un dado, la elección de una carta dentro de una baraja, etc.
Es conocida también como probabilidad matemática, a priori o lógica. La fórmula básica para calcularla es:
Entendiendo por P la probabilidad, por S el número de casos favorables, y por N el número total de casos posibles.
Ejemplo
Con la fórmula podemos calcular la probabilidad de que salga el número que hemos elegido en la ruleta francesa (que consta de 37 números):
Por lo tanto, hay un 2,7% de probabilidad de que acertemos el número de la ruleta francesa.
Probabilidad frecuencial
Es un tipo de probabilidad objetiva, conocido también como frecuentista, que se basa en la frecuencia relativa con la que un evento ocurre en realidad (empíricamente). Es decir, es la proporción de veces que sucede un evento dentro de una serie de repeticiones idénticas o similares.
Por tanto, se considera que un evento es "probable" si tiende a ocurrir con cierta regularidad a medida que se repite el experimento muchas veces.
Se trata de un tipo de probabilidad que solo puede medirse si se dan las condiciones necesarias para realizarlo. Esto implica que en el experimento se puedan controlar todas las variables y observar cómo se desarrollan los resultados en un gran número de repeticiones.
Ejemplo
Podemos hacer uso de la probabilidad frecuencial a la hora de conocer la probabilidad de lluvia en un lugar determinado en un momento determinado del año. Para ello, nos servimos de las mediciones de todas las precipitaciones ocurridas año tras año en la misma fecha en el mismo lugar.
Probabilidad subjetiva
La probabilidad subjetiva es la que se calcula mediante fórmulas o experimentos, pero incluye también elementos basados en la opinión o juicio personal de quien realiza el experimento. Esto se produce porque, en ocasiones, existen elementos no cuantificables que pueden interferir en la probabilidad de que un evento suceda.
A diferencia de las interpretaciones frecuentistas o matemáticas, la probabilidad subjetiva refleja la incertidumbre percibida por una persona en función de su conocimiento y experiencia propios.
Ejemplo
Podríamos usar la probabilidad subjetiva si quisiéramos medir las posibilidades de que un jugador de baloncesto enceste desde un punto x del campo de juego.
Para ello, podríamos utilizar un experimento de probabilidad frecuencial, pero considerar que a medida que el jugador realiza el experimento gana en habilidad. Por tanto, podríamos "inferir" o "presuponer" que cuántas más veces realicemos el experimento, más aumentará la probabilidad de encestar del jugador.
Probabilidad conjunta
La probabilidad conjunta mide la probabilidad de que dos eventos sucedan de forma simultánea. Es decir, que sucedan al mismo tiempo, aunque no guarden una relación estrecha entre sí.
En el contexto de dos eventos (X, Y), la probabilidad conjunta se mediría mediante la siguiente fórmula:
Ejemplo
Con dicha fórmula, podríamos medir, por ejemplo, las posibilidades de que al tirar una moneda al aire y un dado de 6 el resultado fuera cara y 6 al mismo tiempo.
Siendo X las posibilidades de que salga un número concreto del dado e Y las posibilidades de que salga cara o cruz en una moneda, entonces:
El resultado es 0,0833, que equivale a un 8,33% de probabilidad de que ambos eventos sucedan simultáneamente.
Probabilidad marginal
Es el cálculo de las posibilidades que existen de que aparezca un subconjunto de elementos determinado dentro de un conjunto más grande.
La probabilidad marginal permite calcular la probabilidad de un evento en una variable particular sin tener en cuenta las posibles combinaciones de valores de otras variables. Esto puede ser especialmente relevante cuando el objetivo es conocer la probabilidad estadística de una variable específica, sin necesidad de analizar la probabilidad de otras similares.
La fórmula general para la probabilidad marginal de un evento X se calcula mediante la suma de las veces que se ha producido dicho evento dividido entre el número total de datos.
Es decir:
Ejemplo
Un grupo de personas viaja 30 días en un barco. Si anotamos el número de días en que al menos una persona se ha mareado, independientemente del clima y tiempo, tendríamos:
- Días con personas mareadas con sol: 3
- Días con personas mareadas con lluvia: 9
- Días con personas no mareadas con sol: 11
- Días con personas no mareadas con lluvia: 7
Si tomamos la fórmula, podemos realizar el cálculo:
Por lo tanto, cuatro de cada diez días habrá por lo menos alguna persona mareada.
Probabilidad condicional
La probabilidad condicionada o condicional mide las posibilidades que existen de que ocurra un evento, una vez que otro ya ha sucedido.
Se basa en la idea de que estamos restringiendo el espacio muestral al evento Y. En el nuevo espacio muestral que consideramos, evaluamos la probabilidad de X, en relación con las posibilidades dentro de ese espacio muestral reducido.
La fórmula en este caso es:
En el que P(X∩Y) es la probabilidad del evento X cuando se da el evento Y, y P(Y) es la probabilidad del evento Y.
Ejemplo
Imaginemos que el 30% de los miembros de tu familia les gusta jugar al tenis y al fútbol, y el 50% les gusta jugar al fútbol. ¿Qué probabilidades hay de que a un miembro de tu familia al que le guste jugar al fútbol le guste también el tenis?
Apliquemos la fórmula:
Por tanto, la probabilidad de que a un miembro de tu familia le guste también el tenis es del 60%.
Probabilidad bayesiana
La probabilidad bayesiana, basada en la regla de Bayes, mide la probabilidad de una hipótesis en función de una nueva hipótesis dada. Es una forma de razonamiento probabilístico que nos permite ajustar la probabilidad de un hecho en función de la aparición de otro nuevo.
La fórmula clave en la probabilidad bayesiana es la regla de Bayes:
- P(X/Y) es la probabilidad de que suceda X habiendo sucedido Y.
- P(Y/X) es la probabilidad de que suceda Y habiendo sucedido X.
- P(X) es la probabilidad de que suceda X.
- P(Y) es la probabilidad de que suceda Y.
Ejemplo
En una clase hay un 25% de posibilidades de que a un alumno le guste el Quijote, y un 30% de que les guste La Celestina. También se conoce el dato de que si a un alumno le gusta la Celestina, la posibilidad de que le guste El Quijote es del 50%.
La probabilidad bayesiana nos ayuda a saber el porcentaje de posibilidades de que a un alumno que le guste también La Celestina si le gusta El Quijote:
- P(X/Y) es la probabilidad de que te guste La Celestina si te gusta El Quijote.
- P(Y/X) es la probabilidad de que te guste el Quijote si te gusta La Celestina.
- P(X) es la probabilidad de que te guste El Quijote.
- P(Y) es la probabilidad de que te guste La Celestina.
Apliquemos la fórmula:
Por tanto, la probabilidad de que a un alumno le guste La Celestina habiéndole gustado El Quijote es del 41,67%.
Probabilidad geométrica
La probabilidad geométrica nos permite conocer la probabilidad de que un elemento se encuentre en un punto determinado, dentro de un espacio o segmento dado.
La fórmula dependerá del espacio que se está estudiando. Si es una línea, entonces la probabilidad de que un punto se halle dentro un segmento de la línea es:
Ejemplo
Dada una línea de 10 centímetros de longitud, se desea calcular la probabilidad en que un punto se halle dentro de un segmento ubicado en los primeros 3 centímetros.
Si nos servimos de la fórmula, obtenemos lo siguiente:
La probabilidad de que el punto esté en la parte del segmento de 3 centímetros es del 30%.
Vea también Estadística y Frecuencia estadística.
Cómo citar: Significados, Equipo (07/03/2025). "Tipos de probabilidad". En: Significados.com. Disponible en: https://www.significados.com/probabilidad/ Consultado: 4 de abril de 2025, 05:46 am.