Polígono de frecuencia
Un polígono de frecuencia es un recurso gráfico utilizado en estadística para comparar entre sí datos de una o más variables. Suele construirse a partir de un histograma, y se compone de dos ejes y una serie de puntos conectados entre sí mediante líneas rectas.
Por ejemplo, en la imagen de abajo podemos ver la cantidad de personas que asisten a un cine (CinemaLand) a lo largo de la semana. A partir de los datos, vemos en un vistazo rápido que asiste más el sábado, pero no tanto el lunes o miércoles.
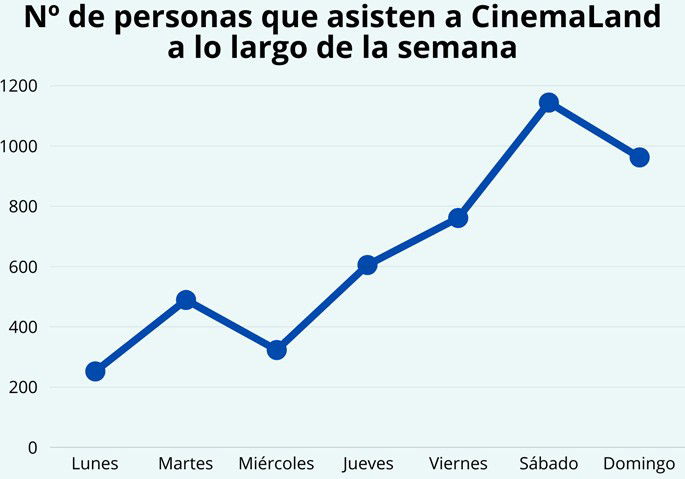
Los polígonos de frecuencia son útiles para comparar variables cuantitativas y ver cuánto varían los datos a lo largo del tiempo o al modificar otra variable. También sirven para identificar visualmente los máximos y mínimos de una serie de datos, así como tendencias.
Se llaman así por presentar vértices y líneas rectas, como sucede con los polígonos en geometría. En algunos casos, un polígono de frecuencia puede servir para representar más de una serie de datos, algo que resulta útil para comparar varios datos a la vez.
Características de un polígono de frecuencia
Un polígono de frecuencia siempre está compuesto por puntos unidos mediante líneas rectas. Eso sí, la presentación puede variar un poco, como por ejemplo, usando cuadrados o triángulos pequeños en vez de puntos.
En un polígono de frecuencia, el punto más alto del gráfico suele ser aquel dato con el valor más alto. Una excepción es en los polígonos de frecuencias acumuladas, ya que el último valor siempre será el más alto.
Los polígonos de frecuencia son una herramienta para representar información cuantitativa, pero no cualitativa. Esto es debido a que este recurso gráfico se construye a partir de números.
Dentro de los polígonos de frecuencia, podemos hablar de los siguientes tres tipos:
- Polígonos de frecuencias absolutas: muestran los datos numéricos tal y como fueron recopilados, sin realizar ninguna modificación o proceso de conversión.
- Polígonos de frecuencias relativas: convierten los datos numéricos a una proporción o ratio, usualmente porcentajes hasta 100%.
- Polígonos de frecuencias acumuladas: cada punto sucesivo de la gráfica es la suma de su propio valor y todos los anteriores, por lo que la gráfica siempre va desde el valor más pequeño hasta el más alto.
Ejemplos de polígonos de frecuencia
Veamos varios ejemplos diferentes de polígonos de frecuencias, ilustrando los diferentes tipos que existen.
Polígono de frecuencias absolutas
Imaginemos un estudio ficticio en el que se recoge cuántos helados de los cinco sabores más populares se venden a lo largo de un día:
- Chocolate: 102
- Caramelo: 38
- Pistacho: 23
- Vainilla: 95
- Oreo: 61
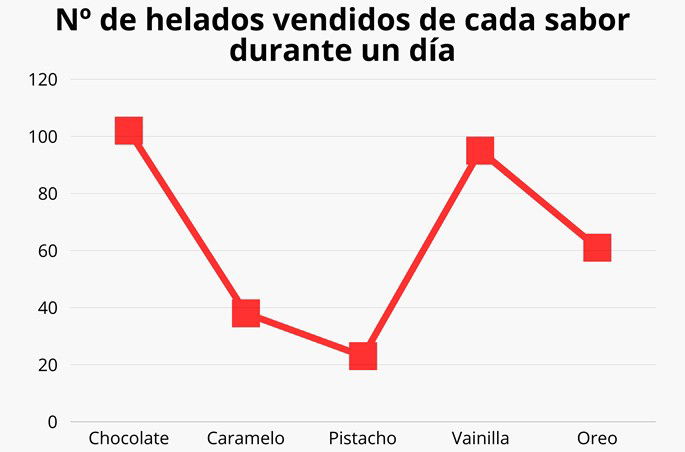
Si echamos un vistazo al polígono de frecuencia, veremos que se venden muchos más helados con sabor a chocolate y vainilla.
Polígono de frecuencias relativas
Pongamos como ejemplo otro estudio ficticio que busca descubrir qué colores prefieren los niños de una localidad. En esta ocasión, en vez de mostrar la cantidad total de los colores elegidos, se decide mostrar el porcentaje de cada color:
- Azul: 21%
- Rojo: 28%
- Verde: 15%
- Rosa: 12%
- Otros colores: 34%
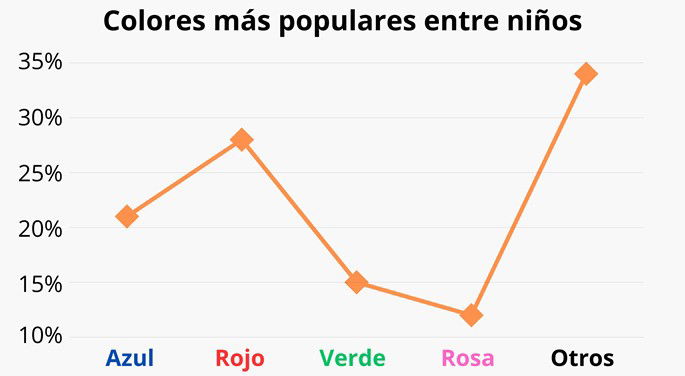
Como los datos mostrados son porcentajes, construimos un polígono de frecuencias relativas. Podemos concluir que el color más preferido es el rojo, seguido del azul.
La categoría "Otros", aunque tenga la proporción alta, agrupa el resto de colores elegidos en menor proporción al color rosa, como el blanco, negro, naranja, etc. Esta es una práctica común para no alargar demasiado el gráfico y enfocarnos solamente en los datos que destacan más.
Polígono de frecuencias acumuladas
Para ilustrar el polígono de frecuencias acumuladas, tomemos el ejemplo anterior de los colores preferidos por los niños. En esta ocasión, lo que haremos es empezar el gráfico desde el 0%, y acumularemos el porcentaje de cada color hasta llegar al 100%.
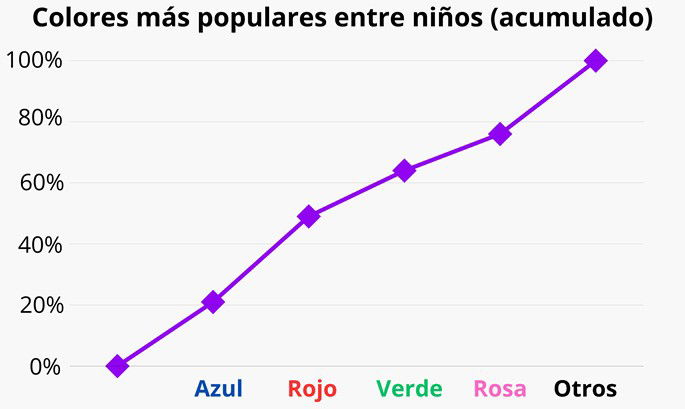
Esta es, simple y llanamente, otra forma de representar los mismos datos. Aunque de un primer vistazo no se ve tan claro qué colores son los más preferidos, sí se puede apreciar que hay un salto más grande hasta azul y rojo comparado con el verde o rosa.
Polígono de frecuencias con más de una serie de datos
En ocasiones, un polígono de frecuencias puede mostrar varias series de datos en un mismo gráfico. Supongamos que se hace un estudio sobre qué instrumento musical se prefiere según la edad.
Al recopilar todos los datos, elaboramos la siguiente tabla:
| Rango de edad | Guitarra | Piano | Violín |
|---|---|---|---|
| 13 a 20 años | 231 | 182 | 87 |
| 21 a 28 años | 290 | 150 | 52 |
| 29 a 35 años | 283 | 187 | 90 |
| 36 a 42 años | 250 | 200 | 104 |
| 42 años o más | 201 | 244 | 136 |
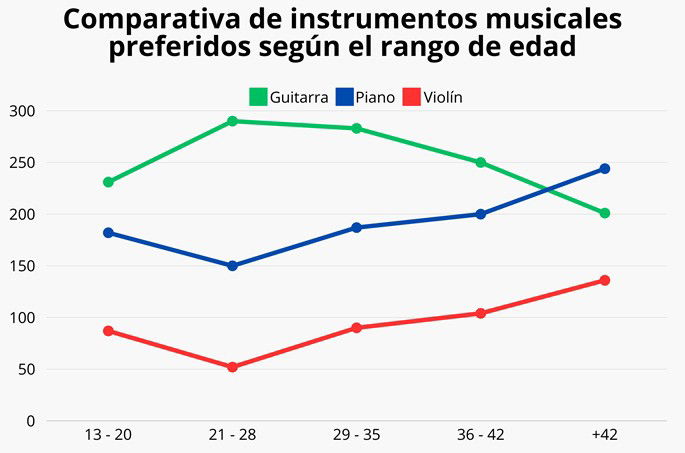
Construimos el polígono de frecuencias para comparar los datos. Nos podemos fijar en un detalle curioso: el interés en la guitarra decae conforme pasan los años, mientras que el interés en el piano y violín crece.
Este tipo de polígonos de frecuencias es muy útil para comparar varios datos entre sí de una forma muy clara y visual.
Cómo hacer un polígono de frecuencias
Para construir un polígono de frecuencias, sigue los siguientes pasos:
- Anota qué datos numéricos vas a representar y las categorías que utilizarás. Por ejemplo, cuánta gente asiste a un cine (datos numéricos) cada día de la semana (categorías).
- Recopila los datos numéricos y categorías en una tabla, ya sea a mano o en una aplicación como Microsoft Excel o Google Sheets.
- Decide cómo vas a ordenar los datos en el gráfico. Por ejemplo, de lunes a domingo.
- Elabora los dos ejes del polígono de frecuencias: el eje vertical se reserva para los datos numéricos, y el horizontal para las categorías.
- Elige el tipo de polígono de frecuencia a utilizar: frecuencias absolutas, relativas o acumuladas. Mira nuestros ejemplos para ver las diferencias entre cada uno.
- Introduce los datos numéricos para cada categoría, representados como puntos.
- Une todos los puntos consecutivos con líneas rectas.
Vea también Estadística y Frecuencia estadística.
Cómo citar: Significados, Equipo (03/01/2025). "Polígono de frecuencia". En: Significados.com. Disponible en: https://www.significados.com/poligono-de-frecuencia/ Consultado: