Matemáticas

Números reales

Equipo de Enciclopedia Significados

Creado y revisado por nuestros expertos

Los números reales, de símbolo R, son el conjunto de números racionales e irracionales, es decir, agrupa todos los números que presentan o no una parte decimal. Estos números son la base del cálculo y análisis matemático, pues nos servimos de ellos para cuantificar, medir y resolver problemas.

Los números reales se expresan de formas distintas. Por ejemplo, un número real puede escribirse como un valor entero (2, -15), cifras con parte decimal (5,41), fracciones (7/3), o raíces (√5).

El conjunto de los números reales y su dominio se representa sobre una recta llamada recta real o recta de números reales:

Recta real de los números reales.

Esta recta no tiene ni principio ni final, ya que existen infinitos números reales positivos y negativos. Cuando hablamos del subconjunto de números reales positivos, el símbolo usado es R⁺; en el caso de los reales negativos, se emplea R^-.

Propiedades de los números reales

Veamos algunas de las propiedades de este conjunto de números.

El dominio de los números reales abarca entre el infinito negativo hasta el infinito positivo, sin incluirlos. Es decir, su dominio es:
$paréntesis izquierdo menos infinito coma infinito paréntesis derecho$
El conjunto de los números reales es integral, es decir, que no hay ningún espacio vacío entre un número del conjunto y otro. Entre los valores 4 y 5 hay otros como 4,1 o 4,6, mientras que entre 4,1 y 4,2 hay más valores, como 4,13 o 4,1592752.
Por lo anterior, podemos deducir que existen infinitos números reales en todo su conjunto, tanto valores negativos como positivos, e incluso entre dos números reales. En el subconjunto [-100, 100] podemos encontrar infinitos números reales, pero también en otros subconjuntos como [0, 100], [0, 10] o [0, 1].
Los números reales comprenden un conjunto totalmente ordenado, cuyo orden no cambia. Por ejemplo, después del 1 viene el 2; después del 1,1 viene el 1,2; tras el 1,11 va el 1,12; y así sucesivamente.
Cualquier suma, resta y multiplicación entre dos números reales siempre devuelve otro número real. También se cumple en todas las divisiones, excepto cuando el denominador del cociente es 0, pues la división entre 0 no está definida en el conjunto.
Las sumas y multiplicaciones de números reales son conmutativas, es decir, que cambiar el orden de los factores no altera el producto.
- 3 + 5 es lo mismo que 5 + 3, pues ambos suman 8.
- 3 x 5 es lo mismo que 5 x 3, ya que el resultado en ambos casos es 15.
Las sumas y multiplicaciones de números reales también son asociativas.
- (3 + 5) + 8 es lo mismo que 3 + (5 + 8), pues ambos dan 16.
- (3 x 5) x 8 es lo mismo que 3 x (5 x 8), pues ambos resultan en 120.
El 0 es el elemento identidad en las sumas y restas de números reales, pues cualquier número sumado a 0 da dicho número. Por ejemplo: 3,3 + 0 = 3,3.
El 1 es el elemento identidad en las multiplicaciones y divisiones (como denominador) de números reales, ya que cualquier número multiplicado o dividido por 1 da dicho número. Por ejemplo: 4 x 1 = 4, y 4 / 1 = 4.
Cada número real tiene su opuesto, o sea, para cada número positivo hay otro del mismo valor pero con signo negativo, y viceversa. Por ejemplo: 10 y -10, -45 y 45, o 2,25 y -2,25.
La raíz de orden par de un número negativo no está definido en el conjunto de los números reales. Por ejemplo, la raíz cuadrada de 2 (√2) sí pertenece al conjunto, pero no la raíz cuadrada de -2 (√-2).

Ver también Números

Más ejemplos de números reales

Existe una amplia variedad de números reales, como:

El cero: 0.
Números enteros positivos: 0, 5, 27, 81, 1027 y 41263.
Números enteros negativos: -8, -40, -555, -3050 y -87654.
Números con decimales finitos: 0,47, 12,78 y -27,904.
Números con decimales periódicos: 1,66666... y -8,636363...
Números con decimales aperiódicos: 0,1234321845... y 6,834967394...

También podemos escribir los números reales como fracciones, radicales o potencias. Veamos unos ejemplos:

$Fracciones dos puntos espacio fracción 5 entre 2 coma espacio fracción 3 entre 10 coma espacio fracción numerador menos 7 entre denominador 4 fin fracción coma espacio fracción 221 entre 234 Radicales dos puntos espacio raíz cuadrada de 2 coma espacio raíz cuadrada de 4 coma espacio raíz cúbica de 9 coma espacio raíz cuadrada de 35 coma espacio raíz quinta de menos 10 fin raíz coma espacio raíz cuarta de 82 Potencias dos puntos espacio 2 elevado a 4 coma espacio 31 elevado a 7 coma espacio 6 elevado a menos 3 fin elevado coma espacio menos 14 elevado a 5$

Vea también Números decimales.

Clasificación de los números reales

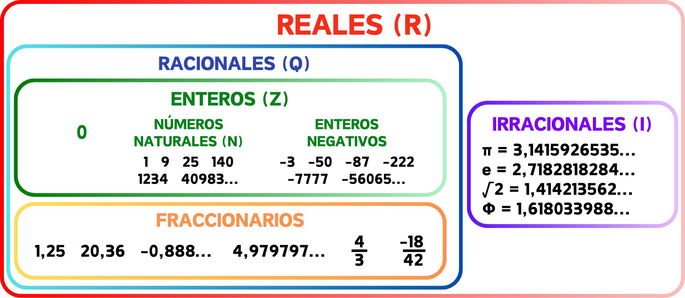
A grandes rasgos, los números reales se dividen en dos subconjuntos: los números racionales y los números irracionales.

El conjunto de los números racionales, denotado como Q, aborda los todos aquellos valores sin expresión decimal y con expresión decimal finita o infinita periódica. Estos números siempre se pueden expresar en forma de fracción como el cociente entre dos números enteros.

Dentro de los racionales hallamos:

Números enteros, que son todas aquellas cifras sin parte decimal. A su vez, los números enteros poseen tres subconjuntos:
- El 0.
- Los números enteros positivos o números naturales.
- Los números enteros negativos.
Números fraccionarios, es decir, cifras con decimales.

El conjunto de los números irracionales, denotado como I, acoge valores con expresión decimal infinita aperiódica. En otras palabras, las cifras decimales no siguen ningún patrón o repetición. Por ello, los números irracionales no se pueden expresar en forma de fracción como el cociente entre dos números enteros.

Vea también Números racionales y Números irracionales.