Números primos

Rafael C. Asth
Revisado por Rafael C. Asth
Profesor de Matemática y Física

Un número primo es aquel que solo tiene dos divisores que dan otro número natural, sin decimales: el 1 y él mismo. Si se divide por cualquier otro número, obtendríamos un número fraccionario, es decir, una cifra con decimales.

El número 7, por ejemplo, es un número primo. Al dividirlo por 1, obtenemos 7, un número natural. Si lo dividimos por 7, el resultado sería 1, otro número natural. No obstante, si dividimos esta cifra por 2, resultaría en un número fraccionario.

fracción 7 entre 1 igual 7 flecha derecha N ú m e r o espacio n a t u r a l fracción 7 entre 7 igual 1 flecha derecha N ú m e r o espacio n a t u r a l fracción 7 entre 2 igual 3 coma 5 flecha derecha N ú m e r o espacio f r a c c i o n a r i o

Lo mismo sucedería si dividiéramos 7 entre 3, 4, 5, 6 o cualquier otro valor mayor a 7. Por lo tanto, como el 1 y 7 son los únicos divisores que resultan en un número natural, sin decimales, confirmamos que 7 es un número primo.

Como aclaración, el 1 no es un número primo. La razón de ello es que solo contiene un divisor: 1. No se puede dividir por ningún otro número para obtener un número natural como resultado. Recuerda que, para considerar un número como primo, la norma establece que ha de tener exactamente dos divisores.

Otros ejemplos de números primos

Veamos unos ejemplos de números para determinar si son primos o no.

Número 5

Comencemos con el 5. Probemos a utilizar varios divisores y comprobemos qué resultados obtenemos:

fracción 5 entre 1 igual 5 flecha derecha N ú m e r o espacio n a t u r a l fracción 5 entre 2 igual 2 coma 5 flecha derecha N ú m e r o espacio f r a c c i o n a r i o fracción 5 entre 3 igual 1 coma 6 con paréntesis de arriba encima flecha derecha N ú m e r o espacio f r a c c i o n a r i o fracción 5 entre 4 igual 1 coma 25 flecha derecha N ú m e r o espacio f r a c c i o n a r i o fracción 5 entre 5 igual 1 flecha derecha N ú m e r o espacio n a t u r a l

Como solo dos divisores menores o iguales a 5 resultan en un número natural, acabamos de comprobar que 5 es un número primo.

Número 11

Probemos a dividir el número 11 por varias cifras, para ver así si hallamos más de dos divisores que den un número natural:

fracción 11 entre 1 igual 11 flecha derecha N ú m e r o espacio n a t u r a l fracción 11 entre 2 igual 5 coma 5 flecha derecha N ú m e r o espacio f r a c c i o n a r i o fracción 11 entre 3 igual 3 coma 6 con paréntesis de arriba encima flecha derecha N ú m e r o espacio f r a c c i o n a r i o fracción 11 entre 4 igual 2 coma 75 flecha derecha N ú m e r o espacio f r a c c i o n a r i o fracción 11 entre 5 igual 2 coma 2 flecha derecha N ú m e r o espacio f r a c c i o n a r i o ... fracción 11 entre 11 igual 1 flecha derecha N ú m e r o espacio n a t u r a l

Por lo tanto, 11 también es un número primo, pues posee solamente dos divisores con los que se obtiene un número natural.

Número 15

Veamos un caso de un número que no es primo, sino compuesto. Si probamos todas las cifras enteras hasta el 15, comprobamos que varias resultan en un número natural:

fracción 15 entre 1 igual 15 flecha derecha N ú m e r o espacio n a t u r a l fracción 15 entre 3 igual 5 flecha derecha N ú m e r o espacio n a t u r a l fracción 15 entre 5 igual 3 flecha derecha N ú m e r o espacio n a t u r a l fracción 15 entre 15 igual 1 flecha derecha N ú m e r o espacio n a t u r a l

Al tener cuatro divisores, el número 15 es un número compuesto. Por tanto, no se considera un número primo.

Listados de números primos

Números del 1 al 200 que son primos

Abajo compartimos una tabla que muestra todos los números del 1 al 200. Los números primos están enmarcados con color verde.

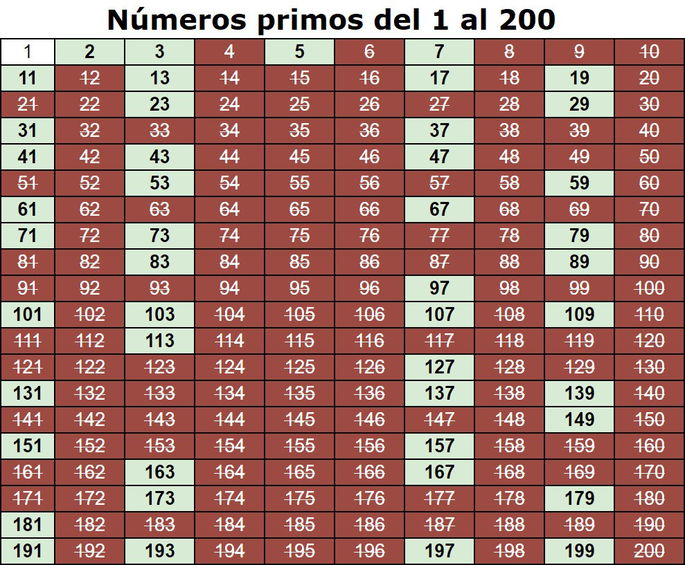
Tabla de los números primos del 1 al 200 resaltados en verde, y números compuestos en rojo y tachados.

En total, hay 46 números primos menores de 200, siendo 199 el último número primo de esta lista. ¿Qué hay de aquellos números primos mayores de 200?

Tabla con los próximos 150 números primos

A continuación, compartimos una tabla con los siguientes 150 números primos mayores a 200, incluyendo algunas cifras mayores a 1000:

211 223 227 229 233 239 241 251 257 263
269 271 277 281 283 293 307 311 313 317
331 337 347 349 353 359 367 373 379 383
389 397 401 409 419 121 431 433 439 443
449 457 461 463 467 479 487 491 499 503
509 521 523 541 547 557 563 569 571 577
587 593 599 601 607 613 617 619 631 641
643 647 653 659 661 673 677 683 691 701
709 719 727 733 739 743 751 757 761 769
773 787 797 809 811 821 823 827 829 839
853 857 859 863 877 881 883 887 907 911
919 929 937 941 947 953 967 971 977 983
991 997 1009 1013 1019 1021 1031 1033 1039 1049
1051 1061 1063 1069 1087 1091 1093 1097 1103 1109
1117 1123 1129 1151 1153 1163 1171 1181 1187 1193

Cómo saber si un número es primo

Hay diversas pistas y maneras que nos ayudan a conocer si un número es primo o no. Para empezar, la cifra ha de ser impar y terminar en 1, 3, 7 o 9. Hay dos razones para ello:

  • Exceptuando el 2, ningún otro número par es primo, pues será divisible por 2. Por lo tanto, podemos descartar cualquier número terminado en 0, 2, 4, 6 u 8.
  • Cualquier número terminado en 5 será divisible por 5, por lo que no puede ser un número primo.

De esta forma, si un número termina en 1, 3, 7 o 9, hay bastantes probabilidades de que sea un número primo. No obstante, conviene hacer una comprobación extra.

Un método útil para saber si un número es primo es dividirlo por otros números primos ya conocidos. ¿Por qué? El motivo es simple: todos los números compuestos, aquellos con más de dos divisores, son resultado del producto de números primos. El 18, por ejemplo, se obtiene multiplicando 2 x 3 x 3.

Aconsejamos memorizar los siguientes números primos: 2, 3, 5, 7, 11 o 13. Gran parte de los números son divisibles por ellos, por lo que es un buen punto de partida para saber si otro número es primo o no.

Características de los números primos

Aquí recopilamos algunas características mencionadas sobre los números primos:

  • Un número primo ha de ser un número natural, es decir, un entero positivo. Los números negativos o fraccionarios no pueden ser números primos.
  • Excepto el 2, todos los números primos son impares.
  • Existe una cantidad infinita de números primos.
  • Todos los números naturales mayores de 1 pueden ser divididos por uno o varios números primos.

Vea también Números naturales y Números enteros.

Diferencia entre números primos y compuestos

Los números compuestos son aquellos que contienen más de dos divisores que devuelven un número natural. Por ejemplo, el 6 posee cuatro divisores naturales, pues se puede dividir entre 1 para dar 6; entre 2 para dar 3; entre 3 para dar 2; y entre 6 para dar 1.

Es decir, mientras que los números primos solo se dividen por 1 y por sí mismos, los compuestos poseen otros divisores.

Para ser número compuesto, ha de tener un número finito de divisores. El 0, al dividirlo por cualquier otro número distinto a 0, siempre devolverá 0. En otras palabras, el 0 contiene infinitos divisores, por lo que no cuenta como número compuesto.

Vea también:

Cómo citar: (04/12/2023). "Números primos". En: Significados.com. Disponible en: https://www.significados.com/numeros-primos/ Consultado:

Rafael C. Asth
Revisado por Rafael C. Asth
Profesor de Matemáticas, licenciado en Estadística y posgraduado en Enseñanza de Matemáticas y Física. Ha sido profesor desde 2006 y crea contenidos educativos en línea desde 2021.
Otros contenidos que pueden ser de tu interés