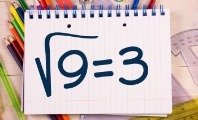Números irracionales
Los números irracionales son números reales con una parte decimal infinita, y que no presenta periodicidad o patrón en la repetición de cifras.
Un número irracional no se puede representar como una fracción o división de dos números enteros, como sucede con los racionales. Es decir, no existe una relación entre un número entero a y otro b que dé como resultado un número irracional.
Veamos unos ejemplos que ilustren la diferencia entre los números irracionales y los racionales con cifras decimales:
Los números irracionales son imposibles de calcular con exactitud, ya que poseen una cantidad infinita de decimales. Por ello, para utilizarlos en fórmulas y operaciones algebraicas, nos servimos de aproximaciones.
I es, en diversas ocasiones, el símbolo utilizado para representar este grupo. Sin embargo, cabe mencionar que los números irracionales no poseen un símbolo oficial, ya que no constituyen una estructura algebraica.
Ejemplos de números irracionales
Hay tres números irracionales utilizados frecuentemente en distintos ámbitos: el número pi, el número de Euler y el número áureo.
- Número pi, con símbolo π y un valor de 3,14159265... Este número marca la relación entre el perímetro de un círculo con su diámetro.
- Número de Euler, con símbolo e y un valor de 2,71828182... Sirve como base de los logaritmos naturales y es común verlo en funciones exponenciales.
- Número áureo o razón de oro, con símbolo φ o Φ y un valor de 1,61803398..., utilizado en artes gráficas.
Además de estos números, es común que las raíces o logaritmos devuelvan números irracionales. Algunos ejemplos son:
- √2, con un valor de 1,41421356...
- √5, con un valor de 2,23606797...
- √8, con un valor de 2,82842712...
- log (5), con un valor de 0,698970004...
- ln (7), con un valor de 1,945910149...
Asimismo, cualquier número con una parte decimal que contenga una sucesión infinita de números aleatorios será irracional, como:
- 27,7837681293...
- -5,482076018631...
- 0,102004200032...
Vea también Símbolo Pi (π) y Números decimales.
Características y propiedades de los números irracionales
- Dado que los números irracionales tienen infinitas cifras decimales, son imposibles de calcular con exactitud.
- Multiplicar, dividir, sumar y restar dos números irracionales siempre resulta en otro número irracional. Las excepciones son: dividir un número irracional por sí mismo, pues daría 1; y restar un número irracional por sí mismo, por lo que daría 0.
- Multiplicar, dividir, sumar y restar un número irracional con otro racional diferente de 0 resulta en un número irracional.
- Los números irracionales llenan los espacios vacíos de la recta real que hay entre números racionales. Por lo tanto, la recta real está compuesta por números racionales e irracionales.
- Entre dos números racionales existe una cantidad infinita de números irracionales. Por ejemplo, entre 2 y 3 hay infinitos números irracionales, pero también entre 2,1 y 2,2.
Ver también Números
Clasificación de los números irracionales
Los números irracionales pertenecen a los números reales y, a su vez, los números complejos. Difieren de los números racionales en que no podemos conocer todas las cifras decimales.
Dentro de los números irracionales podemos hablar de algebraicos y trascendentales:
- Números irracionales algebraicos: engloba los números que son raíces de polinomios diferentes a cero. Por ejemplo, el número áureo es un número algebraico, pues es una raíz del polinomio x2 - x - 1.
- Números irracionales trascendentales: engloba los números que no son raíces de ningún polinomio con coeficientes racionales, por lo que no son solución de ecuaciones algebraicas. Dos ejemplos de números trascendentales son el número pi y el número e.
Vea también Números racionales y Números reales.
También te puede interesar:
Cómo citar: Significados, Equipo (12/12/2023). "Números irracionales". En: Significados.com. Disponible en: https://www.significados.com/numeros-irracionales/ Consultado: