Números complejos
Los números complejos, de símbolo C, son un grupo que engloba todos los tipos de números que conocemos, sean enteros, fraccionarios, naturales o imaginarios. Es, por ello, la categoría más alta en la clasificación de números.
A su vez, los números complejos son una combinación de otros dos grupos: los números reales (R) y los números imaginarios. Como tal, un número complejo suele representarse con la fórmula Z = A + Bi, en la que:
- Z es el número complejo;
- A, o Re(Z), corresponde a la parte real del número complejo, que puede ser entero o fraccionario;
- Bi, o Im(Z), corresponde a la parte imaginaria, compuesto por un número real B y el número imaginario i, que equivale a √-1.
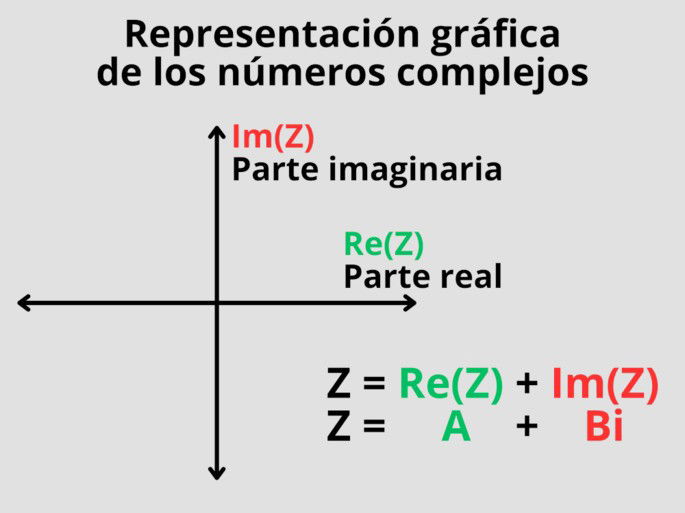
Esta fórmula se conoce como forma binómica, y con ella podemos representar los números complejos de forma gráfica. Para ello, nos servimos del plano complejo, en el que el eje de las abscisas corresponde a la parte real, y el eje de ordenadas, la parte imaginaria.
Los números imaginarios se descubrieron ante la necesidad de abarcar las raíces de números negativos, pues estas raíces no entran dentro de la recta real. En este sentido, los números complejos reflejan todas las raíces de los polinomios.
René Descartes fue el primero en introducir la idea de los números imaginarios. Más adelante, en el siglo XVI, el matemático italiano Gerolamo Cardano demostró poder solucionar ecuaciones teniendo un término negativo dentro de una raíz cuadrada.
Tomando como base la demostración de Gerolamo, Carl Friedrich Gauss consolidó la idea y desarrolló un tratado sobre los números complejos, incluyendo así la parte real y la imaginaria.
Ejemplos y operaciones de números complejos
A continuación, te mostramos varios ejemplos de números complejos en su forma binómica:
Podemos usar números complejos para realizar operaciones matemáticas, sean sumas, restas, multiplicaciones o divisiones. Vea los siguientes ejemplos:
Características de los números complejos
- El conjunto de todos los números complejos se representa con la letra C, y conforman un espacio vectorial de dos dimensiones que contienen números reales e imaginarios en dos ejes cartesianos distintos.
- A diferencia de los números reales, los complejos sí incluyen todas las raíces de polinomios.
- Cuando un número complejo no presenta una parte real, se compone solamente de una parte imaginaria pura: Z = Bi.
- El número imaginario, simbolizado como i, equivale a √-1, y siempre multiplica un número real para formar la parte imaginaria de un número complejo.
- Toda operación matemática que contenga un número complejo siempre resultará en otro número complejo.
Para qué sirven los números complejos
Los números complejos se emplean mucho para representar ondas electromagnéticas y corrientes eléctricas. Por lo tanto, el campo de la electrónica, telecomunicaciones y la ingeniería industrial se benefician mucho de este tipo de números.
Además, esta clase de números son una herramienta de trabajo habitual en álgebra, análisis y en diferentes ramas de las matemáticas. Los números complejos pueden aparecer al trabajar con ecuaciones diferenciales, y su presencia puede facilitar el cálculo de algunas integrales.
Otros ámbitos en los que se utilizan los números complejos son la aerodinámica y la hidrodinámica, así como en la mecánica cuántica y otros campos de la física.
Vea también:
Cómo citar: (17/12/2024). "Números complejos". En: Significados.com. Disponible en: https://www.significados.com/numeros-complejos/ Consultado:
