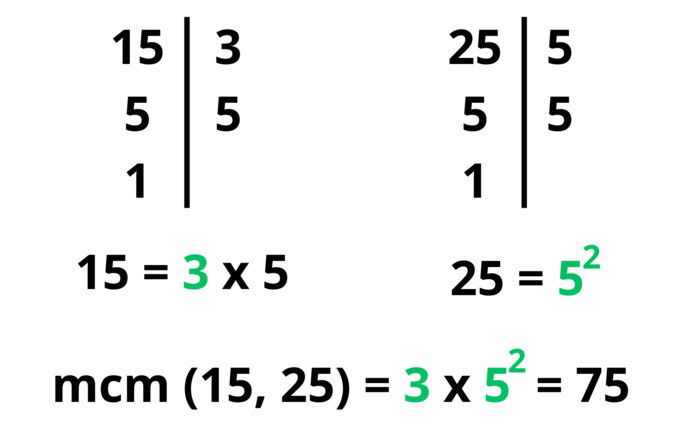Mínimo común múltiplo (mcm)
El mínimo común múltiplo, también conocido como mcm o m.c.m., es el menor múltiplo que hay entre dos o más números naturales. En otras palabras, es el primer valor, el más pequeño, que puede ser dividido por dichos números.
El mínimo común múltiplo lo denotamos como mcm(a, b) = x, en el que:
- a y b son los números naturales, y
- x es el múltiplo más pequeño que puede ser dividido tanto por a como por b.
Pongamos como ejemplo los números 2 y 3. Si completamos la tabla de multiplicar de ambos números, hallaremos sus múltiplos. En el caso de 2, sus múltiplos son 2, 4, 6, 8, 10, etc., y los múltiplos de 3 son 3, 6, 9, 12, 15, etc. Si nos fijamos en los múltiplos de ambos, veremos que hay uno en común: el 6.
Por lo tanto, el mínimo común múltiplo de 2 y 3 es 6. Esto lo representamos de la siguiente forma: mcm(2, 3) = 6.
El mcm se puede calcular para la cantidad de números que uno quiera. Usualmente, se realiza para dos o tres números, pero es posible hacerlo para cuatro o más.
El mínimo común múltiplo tiene varias aplicaciones en matemáticas. Una de ellas es en la suma y resta de fracciones, pues es necesario que las fracciones contengan el mismo denominador. Para lograr un mínimo denominador común en todas las fracciones, se toman todos los denominadores y se calcula el mcm.
Cómo sacar el mínimo común múltiplo
Hay tres métodos que podemos emplear para sacar el mínimo común múltiplo de varios números naturales. Por un lado, podemos hallar el mcm escribiendo los múltiples de cada número natural. Por el otro lado, podemos descomponer los números naturales en factores primos. Por último, si los números naturales son primos, solo debemos multiplicar entre ellos.
Primer método para sacar el mcm
El primer método de anotar los múltiplos de cada número se emplea cuando queremos descubrir el mínimo común múltiplo de dos números naturales pequeños.
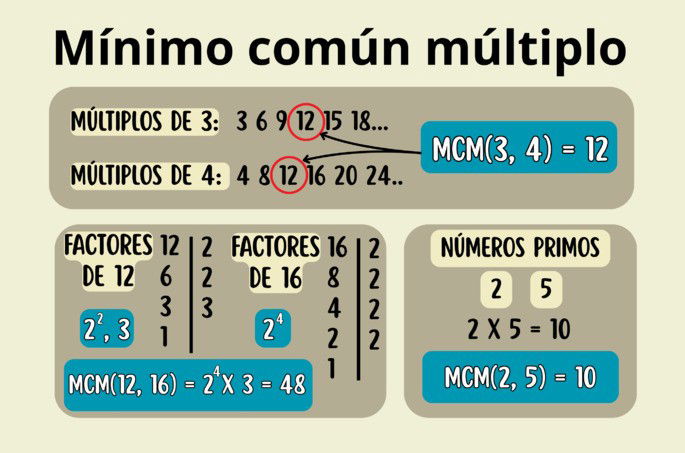
Imaginemos que buscamos el mínimo común múltiplo de 3 y 4. Primero, vamos a anotar los primeros diez múltiplos de ambos números, como si escribiésemos las tablas de multiplicar:
- Múltiplos de 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Múltiplos de 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40...
Anotados los múltiplos, el siguiente paso es ver cuáles son comunes. En este caso, tanto 12 como 24 son múltiplos de 3 y 4. Finalmente, nos queda ver cuál es el mínimo; como 12 es más pequeño que 24, tomamos el 12 como el mínimo.
Concluimos entonces que: mcm(3, 4) = 12.
Segundo método para sacar el mcm
El segundo método inicia con la descomposición de los números naturales en números primos, y se suele utilizar cuando los números son grandes. Para descomponer, se dividen las cifras por números primos todas las veces que sea posible, siempre que no resulte en números decimales. Comenzamos dividiendo por 2, luego por 3, por 5, por 7, por 11, etc., hasta que el resultado sea 1.
Pongamos como ejemplo los números 12 y 16. Para hallar el mcm, empezamos descomponiendo estas cifras en números primos. Recuerda dividir primero por 2 todas las veces que puedas, hasta que el resultado no sea un número entero. Entonces, pasamos al siguiente número primo, 3, como divisor.

Los factores de 12 son 22 y 3, mientras que el único factor de 16 es 24. Hallados los factores para ambos números, debemos identificar los factores que tengan el mayor exponente; en este caso, son 24 y 3. A continuación, multiplicamos estos factores, y con ello obtenemos el mínimo común múltiplo.
En conclusión: mcm(12, 16) = 48.
Tercer método para sacar el mcm
El último método es el más sencillo de todos. Si sabemos que los números con los que queremos calcular el mcm son números primos, lo único que debemos hacer es multiplicar los números primos. Esto es debido a que los números primos son solo divisibles por 1 y por sí mismos, y no se pueden descomponer en otros números primos.
Por ejemplo, buscamos hallar el mínimo común múltiplo de 2 y 5. Tanto 2 como 5 son números primos, por lo que ya no se pueden descomponer más. En este caso, solo debemos multiplicar 2 por 5, que resulta en 10.
Por tanto: mcm(2, 5) = 10.
Ejemplos del mínimo común múltiplo
A continuación presentamos una serie de ejercicios resueltos empleando los tres métodos comentados anteriormente.
Ejercicio 1
Halla el mínimo común múltiplo de los números 5 y 6.
Ejercicio 2
Encuentra el mínimo común múltiplo de los números 15 y 25.
Ejercicio 3
Deduce cuál es el mínimo común múltiplo de los números 7 y 11.
Ejercicio 4
Halla el mínimo común múltiplo de 4, 6 y 8.
Ejercicio 5
Encuentra el mínimo común múltiplo de 30, 45 y 54.
Vea también Ejercicios de mcm y MCD y Suma de fracciones.
Cómo citar: Rhoton, Stephen (04/04/2025). "Mínimo común múltiplo (mcm)". En: Significados.com. Disponible en: https://www.significados.com/minimo-comun-multiplo-mcm/ Consultado: