Máximo común divisior (MCD)
El máximo común divisor o MCD es el mayor valor por el que pueden dividirse a la vez dos o más números enteros. Para que esto sea posible, el divisor ha de ser un factor o divisor positivo y común entre los números a determinar el MCD, y el resto de la división ha de ser cero.
El máximo común divisor lo denotamos como MCD(a, b) = c, en el que:
- a y b son los números enteros a calcular su MCD, y
- c es el divisor más grande por el que los números enteros a y b pueden dividirse.
Pongamos como ejemplo los números 8 y 12. Sabemos que 8 se puede dividir entre 1, 2, 4 y 8 sin que nos quede un resto en la división. Si analizamos el 12, veremos que sus factores son 1, 2, 3, 4, 6 y 12.
Los factores comunes de 8 y 12 son 1, 2 y 4. No obstante, el MCD nos pide que hallemos aquel divisor común que sea de mayor valor. Como 4 es el factor más grande, concluimos que el MCD de 8 y 12 es: MCD(8, 12) = 4.
El MCD sirve para simplificar ecuaciones y fracciones. De esta forma, manejamos operaciones con números más pequeños, facilitando los cálculos. Otros usos del MCD son calcular el mínimo común múltiplo o mcm de dos números, o la resolución de algunos tipos de ecuaciones, como la ecuación diofántica lineal o la pitagórica.
Cómo sacar el máximo común divisor
Existen tres formas de calcular el máximo común divisor de dos números enteros o más. Las explicamos abajo.
Primer método para sacar el MCD
El primer método para hallar el MCD es escribiendo todos los divisores o factores que contenga cada número. Luego se identifican los factores comunes, y finalmente se toma el factor común más alto. Recuerda que para que un número sea divisor de otro, el resultado de la división ha de ser cero, es decir, no puede haber cifras decimales.
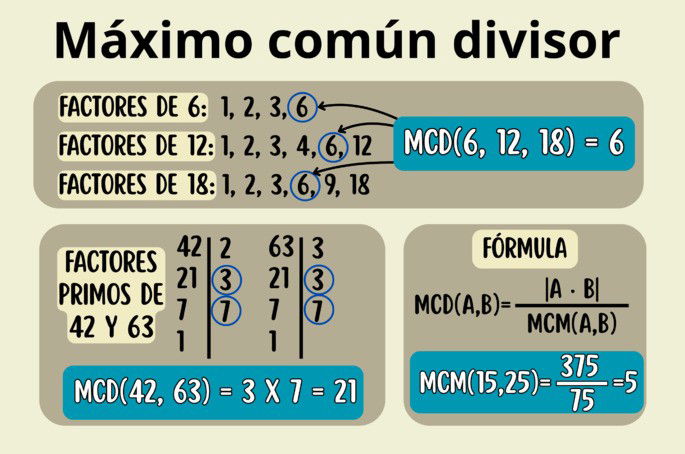
Pongamos como ejemplo que deseamos calcular el MCD de 6, 12 y 18. El primer paso es anotar todos los divisores para cada número:
- Divisores de 6: 1, 2, 3, 6.
- Divisores de 12: 1, 2, 3, 4, 6, 12.
- Divisores de 18: 1, 2, 3, 6, 9, 18.
El segundo paso es identificar los divisores comunes para los tres números; en este caso son 1, 2, 3 y 6. El último paso es tomar el factor más alto, que aquí es 6. Por tanto: MCD(6, 12, 18) = 6.
Segundo método para sacar el MCD
La segunda forma de encontrar el máximo común divisor es mediante la descomposición por factores primos. Tras realizar la descomposición para cada número, se identifican los factores comunes y luego se multiplican estos para hallar el MCD.
Para ilustrar este método, veamos el siguiente ejemplo, en el que calculamos el MCD para los números 42 y 63:

Los factores primos de cada número son:
- Factores primos de 42: 2, 3 y 7.
- Factores primos de 63: 3, 3 y 7.
Los que coinciden son los números primos 3 y 7. Multiplicamos estas dos cifras, y con ello sacamos el máximo común divisor, 21. Es decir: MCD(42, 63) = 21.
Tercer método para sacar el MCD
El último método para calcular el MCD es utilizando la fórmula que lo relaciona con el mcm o mínimo común múltiplo. El mcm es el valor más pequeño que es múltiplo de dos o más números.
La fórmula es:
En el que:
- MCD(a, b) corresponde al máximo común divisor de los números a y b;
- mcm(a, b) corresponde al mínimo común múltiplo de los números a y b; y
- |a x b| es el valor absoluto del producto entre a y b.
Imaginemos que debemos calcular el máximo común divisor de 15 y 25. Al mirar los múltiplos de ambos números, el primer múltiplo que coincide es 75; por lo tanto, este es el mínimo común múltiplo de 15 y 25.
Procedemos con la fórmula:
El máximo común divisor de 15 y 25 es 5.
Te puede interesar Mínimo común múltiplo (mcm).
Ejemplos del máximo común divisor
Abajo compartimos unos ejercicios resueltos del cálculo del máximo común divisor, empleando las diferentes metodologías presentadas en este artículo.
Ejercicio 1
Halla el MCD de 9, 12 y 21 usando el primer método (anotando todos los factores para cada número).
Ejercicio 2
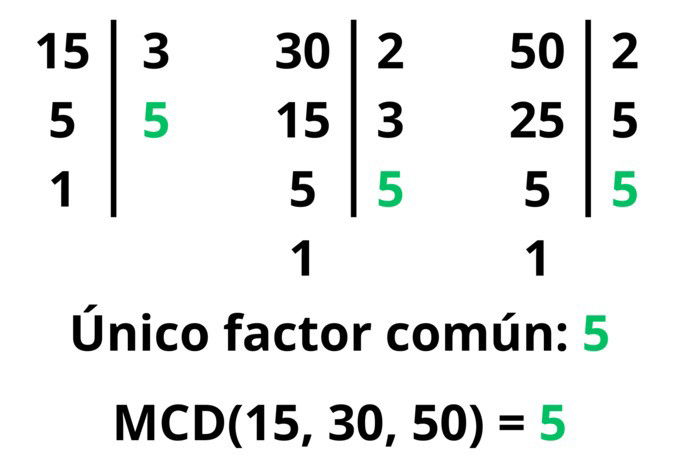
Encuentra el MCD de 15, 30 y 50 empleando el segundo método (descomposición por factores primos).
Ejercicio 3
Descubre cuál es el MCD de 72 y 96, sabiendo que el mcm (mínimo común múltiplo) de ambos es 288.
Ejercicio 4
Obtén el MCD de 14, 28 y 35.
Ejercicio 5
Calcula el MCD de los siguientes números: 60, 72, 84.
Vea también Ejercicios de mcm y MCD.
Cómo citar: Rhoton, Stephen (08/04/2025). "Máximo común divisior (MCD)". En: Significados.com. Disponible en: https://www.significados.com/maximo-comun-divisior-mcd/ Consultado: