Logaritmo
El logaritmo de un número es el exponente que hay que elevar a una base para que nos dé dicho número. Se trata de la operación inversa de la potenciación, ya que el logaritmo del número indica el exponente por el cual se debe elevar la base para obtener la potencia.
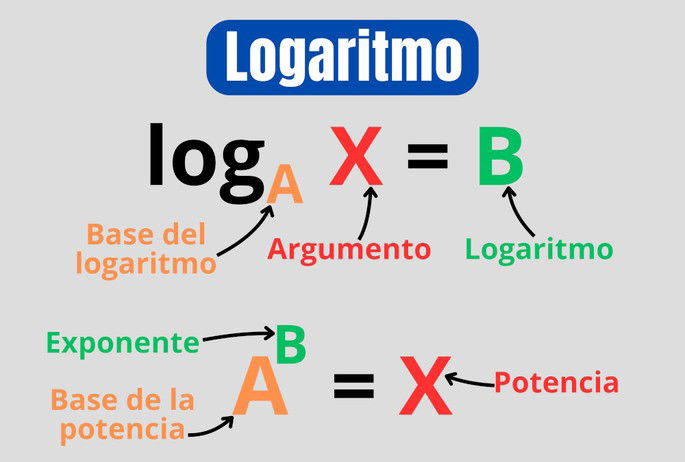
Al proceso de calcular el logaritmo se le llama logaritmación, y generalmente se representa de la siguiente forma: logA X = B. Retomando la definición, el logaritmo de un número (X) es el exponente (B) que hay que elevar a la base (A).
Por lo tanto, las diferentes partes son:
- log, el indicador de que la operación matemática es el cálculo de un logaritmo;
- A, la base del logaritmo, que siempre ha de ser un número positivo;
- X, el argumento o número al que se aplica la operación logarítmica;
- B, el logaritmo de la operación matemática.
Por ejemplo, si tenemos un logaritmo como log3 9 = 2, esto nos indica que 3 es la base del logaritmo, 9 el argumento, y 2 el logaritmo.
La inversa del logaritmo es la potenciación. Si seguimos con el ejemplo, la operación de potenciación sería 32 = 9. De esta forma, se puede establecer una correlación entre las diferentes partes de un logaritmo y la potenciación:
- Base del logaritmo ⬌ Base de la potencia
- Argumento del logaritmo ⬌ Potencia
- Logaritmo ⬌ Exponente
Existen diversos tipos de logaritmos. Uno de los más comunes es el logaritmo decimal, que se expresa como aquel logaritmo en base 10. También podemos hablar de los logaritmos naturales, cuya base es el número de Euler o e.
John Napier fue el primero que introdujo los logaritmos durante el siglo XVII, que sirvió para simplificar varios cálculos. Más adelante, en el siglo XVIII, Leonhard Euler introdujo el número de Euler o e, y conectó los logaritmos con la función exponencial.
Propiedades de los logaritmos
Los logaritmos tienen algunas propiedades que se deben tener en consideración para que sean más fáciles de resolver.
Una de las más importantes es que la base del logaritmo siempre ha de ser un número positivo diferente a 1. Es decir, no puede ser ni cero ni un número negativo. Tampoco existen los logaritmos cuyo argumento sea negativo, es decir, logA X = B cuando X < 0.
Además, debemos tener en cuenta las siguientes propiedades de los logaritmos:
- Si para un logaritmo logA X = B, el argumento (X) y la base (A) son el mismo, entonces el logaritmo (B) es 1.
- El logaritmo de 1 siempre es igual a 0, sin importar la base. Esto es debido a que cualquier número elevado a 0 da 1.
- El logaritmo de un producto es igual a la suma de los logaritmos de los factores del producto: logA (X·Y) = logA X + logA Y.
- El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador: logA (X÷Y) = logA X - logA Y.
- El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base: logA (XY) = Y·logA X.
- El logaritmo de una raíz es igual al cociente del logaritmo del radicando y el índice de la raíz: logA √X = (logA X)÷Y.
Tipos de logaritmos y ejemplos
Existen tres tipos de logaritmos, los cuales son el logaritmo natural, decimal y binario.
Un logaritmo natural es aquel cuya base es el número e (el número de Euler), que equivale a 2,718281828. En vez de representarlo como loge X, se suele escribir como ln o L.
Por ejemplo, ln 45 = 3,8067. Si realizamos la operación de potenciación, veremos que nos da el mismo argumento: e3,8067 = 45.
Un logaritmo decimal es aquel cuya base es el número 10. Para simplificar la notación, es habitual que los logaritmos decimales se expresen sin mostrar el número, es decir, como log X. Por lo tanto, no es necesario poner el número 10 como base en logaritmos decimales, solo cuando la base es otro número distinto a 10.
Por ejemplo, log 1000 = 3, ya que si elevamos 103, resulta en la cifra 1000. Otro ejemplo es log 5 = 0,699.
Un logaritmo binario es aquel cuya base es el número 2, y se puede representar como lg o ld. No obstante, es habitual mostrar este logaritmo como log2 X.
Un par de ejemplos son log2 16 = 4, ya que 24 es igual a 16, y log2 128 = 7, pues 27 es igual a 128.
Vea también:
Cómo citar: Significados, Equipo (13/02/2025). "Logaritmo". En: Significados.com. Disponible en: https://www.significados.com/logaritmo/ Consultado: