Ley de los signos
La ley de los signos es un principio fundamental en las matemáticas que establece cómo interactúan los signos de los números al realizar operaciones matemáticas, como la suma, resta, multiplicación y división.
Dichos signos son el signo + (positivo), que indica que un número es mayor que cero, y el signo - (negativo), que indica que un número es menor que cero.
La ley de los signos se utiliza principalmente en las operaciones de multiplicación y división. En estas operaciones, el resultado de combinar dos números depende de los signos de dichos números.
-
(+) × (+) = (+)
-
(−) × (−) = (+)
-
(+) × (−) = (−)
-
(−) × (+) = (−)
Este principio sigue una regla básica:
- Signos iguales dan un resultado positivo.
- Signos diferentes dan un resultado negativo.
Es decir, cuando ambos números tienen el mismo signo, el resultado es positivo. Y cuando tienen signos opuestos, el resultado es negativo.
La ley de los signos establece qué signo llevará el número resultante de una operación entre números positivos y negativos. Es esencial comprender y aplicar esta ley correctamente para resolver ecuaciones y realizar operaciones básicas con números enteros.
Aunque se utiliza principalmente en las operaciones de multiplicación y división, también tiene implicaciones en la suma y la resta de números con diferentes signos.
Dado que la ley de los signos es un componente esencial en la resolución de operaciones matemáticas, es importante memorizarla para poder aplicarla de manera eficaz.
Ley de los signos en la suma y la resta
En las operaciones de suma, el signo del resultado depende de los valores absolutos de los números involucrados y sus signos. Las reglas básicas son:
- Positivo + Positivo = Positivo (+) + (+) = (+)
- Negativo + Negativo = Negativo (−) + (−) = (−)
- Positivo + Negativo (o Negativo + Positivo): en este caso, al número con mayor valor absoluto se le resta el valor menor, y el signo del resultado será el del número con mayor valor absoluto.
La resta sigue las mismas reglas que la suma, ya que restar es lo mismo que sumar el opuesto de un número. Del mismo modo, el signo del resultado va a depender de los valores absolutos:
-
Positivo − Positivo = Positivo o Negativo, dependiendo de los valores (+) − (+) = (+) o (−)
-
Negativo − Negativo = Negativo o Positivo, dependiendo de los valores (−) − (−) = (−) o (+)
Ley de los signos en la multiplicación
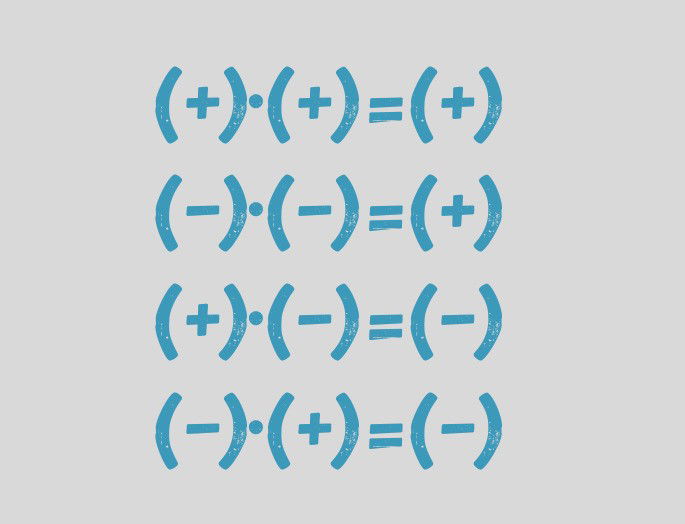
La ley de los signos es especialmente clara en las operaciones de multiplicación y división, donde se aplican estas reglas directamente:
Signos iguales (positivo con positivo o negativo con negativo) siempre resultan en un número positivo.
Signos diferentes (positivo con negativo o negativo con positivo) siempre resultan en un número negativo.
- Positivo × Positivo es Positivo (+) × (+) = (+)
- Negativo × Negativo es Positivo (−) × (−) = (+)
- Negativo × Positivo es Negativo (−) × (+) = (−)
- Positivo × Negativo es Negativo (+) × (−) = (−)
Ver también: Multiplicación, Leyes de los exponentes y Leyes de los exponentes y radicales
Ley de los signos en la división
La ley de signos en la división opera de la misma manera que en la multiplicación:
- Positivo ÷ Positivo = Positivo (+) ÷ (+) = (+)
- Negativo ÷ Negativo = Positivo (−) ÷ (−) = (+)
- Positivo ÷ Negativo = Negativo (+) ÷ (−) = (−)
- Negativo ÷ Positivo = Negativo (−) ÷ (+) = (−)
Referencias:
Díaz Mora, H. F. (2015). La ley de los signos: Una propuesta para la enseñanza-aprendizaje de la multiplicación de números enteros
Suárez, M. (2004). Interaprendizaje holístico de matemática. Ibarra, Ecuador: Gráficas Planeta.
Saber más sobre:
Cómo citar: Significados, Equipo (29/09/2025). "Ley de los signos". En: Significados.com. Disponible en: https://www.significados.com/ley-de-los-signos/ Consultado: