Identidades trigonométricas
Las identidades trigonométricas son ecuaciones que relacionan funciones trigonométricas, y que son válidas para todos los valores del ángulo. Para que se den estas identidades, solo debe existir una variable: el ángulo.
Un ejemplo de identidad trigonométrica es la relación entre el seno y la cosecante de un ángulo:
Esta ecuación sirve como punto de partida para establecer que el seno es la función inversa de la cosecante, y viceversa. La relación siempre se cumple para todo valor del ángulo alfa (α); es por ello que se trata de una identidad trigonométrica.
Las identidades trigonométricas fundamentales son las recíprocas, pitagóricas y las identidades por cociente. Además de estas tres, podemos establecer otras según las funciones y ángulos empleados.
Identidades recíprocas
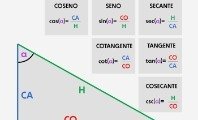
Las identidades recíprocas relacionan las funciones trigonométricas entre sí. En concreto, existen tres:
- El seno como función inversa de la cosecante, y viceversa.
- El coseno como función inversa de la secante, y viceversa.
- La tangente como función inversa de la cotangente, y viceversa.
A partir de estas relaciones, las identidades recíprocas se representan con las siguientes fórmulas:
Identidades pitagóricas
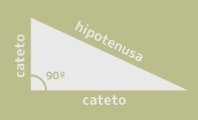
Las identidades pitagóricas se llaman así al ser relaciones entre funciones trigonométricas similares al teorema de Pitágoras. Este teorema determina la relación entre los catetos e hipotenusa de un triángulo rectángulo como:
Siendo A y B los catetos del triángulo, y H su hipotenusa. Al trazar triángulos rectángulos en el círculo trigonométrico, de ahí podemos sacar las siguientes identidades pitagóricas:
Vea también Teorema de Pitágoras.
Identidades por cociente
Las identidades por cociente son otro tipo de identidades que relacionan las funciones trigonométricas entre sí. En este caso, las identidades parten de las definiciones de tangente y cotangente, calculadas a partir del cociente entre el seno y el coseno.
Las identidades por cociente son:
Aquí también podemos ver cómo la tangente es la función inversa de la cotangente.
Otras identidades trigonométricas
Identidades de cofunción
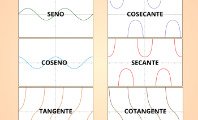
Las identidades de cofunción son pares de funciones que relacionan la función trigonométrica de un ángulo con la del complemento de dicho ángulo. Además, estos pares de funciones poseen una evolución similar cuando se describen en el plano cartesiano unitario.
Las identidades de cofunción son:
Para ver cómo evolucionan las diferentes funciones en el plano cartesiano unitario, vea Funciones trigonométricas.
Identidades de ángulos opuestos
La identidad de los ángulos opuestos tiene que ver con la paridad de la función trigonométrica, que no es más que la presencia o ausencia de simetría de la función en el plano cartesiano.
Las identidades pares, aquellas funciones que presentan simetría respecto al origen de coordenadas, son:
Las identidades impares, aquellas funciones que no presentan simetría, son:
Identidades de suma y resta de ángulos
Si conocemos el valor del seno, coseno o tangente para ángulos concretos, nos podemos servir de las identidades de suma y resta. Estas identidades surgen a partir de descomponer un ángulo en dos, de forma que podemos obtener ángulos conocidos y facilitar nuestro cálculo.
Por ejemplo, si no conocemos el seno y coseno de 150º, pero sí los de 240º y 90º, podemos reescribir el ángulo como 240º - 90º y realizar los cálculos.
Las identidades de suma de ángulos para el seno, coseno y tangente son:
Mientras que las identidades de resta de ángulos son:
Identidades de ángulo doble
Las identidades de ángulo doble surgen a partir de las relaciones de suma y diferencia de ángulos, pero los dos ángulos iguales. Por ejemplo, si no conocemos el valor de una función trigonométrica para un ángulo de 120º, pero sí para 60º, conviene emplear este tipo de identidad.
Las identidades de ángulo doble para el seno, coseno y tangente son:
Además, también podemos determinar identidades de ángulo doble para la cosecante, secante y cotangente, que son:
Vea también Razones trigonométricas y Trigonometría.
Cómo citar: Significados, Equipo (26/02/2024). "Identidades trigonométricas". En: Significados.com. Disponible en: https://www.significados.com/identidades-trigonometricas/ Consultado: