Hipotenusa
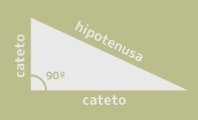
La hipotenusa es el lado opuesto al ángulo recto de un triángulo rectángulo, y además, el lado más largo de dicho triángulo. El ángulo recto es aquel de 90º que une en un vértice los dos catetos del triángulo rectángulo.
Podemos ver la hipotenusa representada en la siguiente imagen:
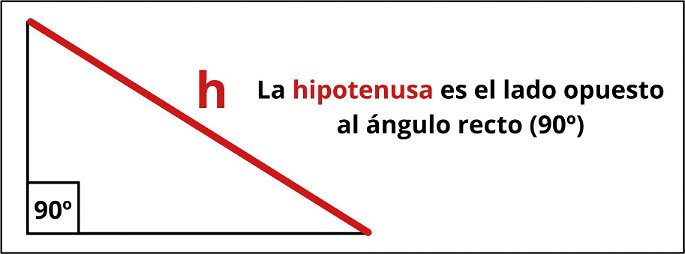
La hipotenusa se une a los dos catetos en dos vértices distintos, formando un ángulo agudo (menor de 90º) con cada uno de ellos. Debido a la existencia del ángulo recto, por más grandes que sean los catetos, la hipotenusa siempre será el lado más largo del triángulo rectángulo.
La hipotenusa es un concepto que solo existe en triángulos rectángulos. Si un triángulo no posee un ángulo recto, no hablaremos de hipotenusa ni de catetos, sino de lados del triángulo. Por ello, es preciso que exista un ángulo recto.
Hay una serie de relaciones entre la hipotenusa, catetos y ángulos que podemos aprovechar para calcular la hipotenusa. Veámoslas a continuación.
Cómo sacar la hipotenusa
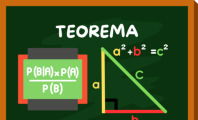
La hipotenusa se puede calcular de diferentes maneras dependiendo de los datos que conozcamos. La forma tradicional es a través del Teorema de Pitágoras, sirviéndonos de la medida de los catetos.
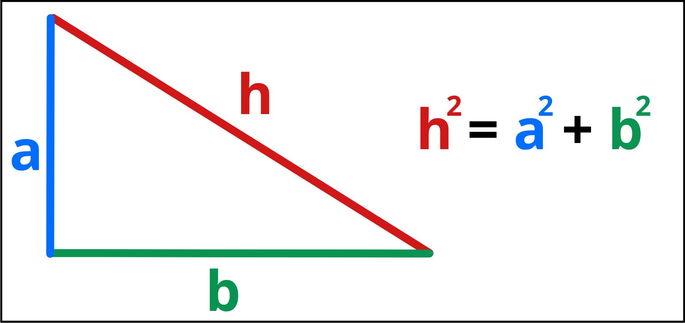
El teorema establece que, en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. O sea:
En el que:
- h corresponde a la hipotenusa.
- a y b corresponden a los catetos adyacentes al ángulo recto.
De esta forma, podremos calcular la hipotenusa de forma sencilla siempre que conozcamos el valor de ambos catetos.
Vea también Teorema de Pitágoras.
Métodos alternativos para calcular la hipotenusa
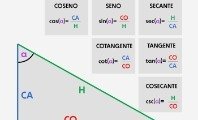
Ahora, si solo conocemos el valor de un cateto, podemos calcular la hipotenusa si también sabemos todos los ángulos. Para ello, nos serviremos de las razones trigonométricas seno y coseno.
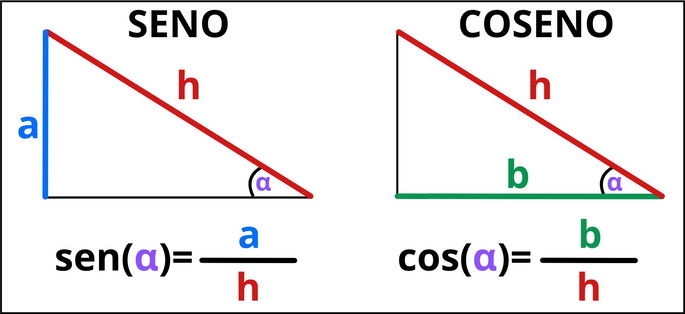
El seno de un ángulo dentro de un triángulo rectángulo es la relación entre el cateto opuesto al ángulo y la hipotenusa:
Por otro lado, el coseno de un ángulo es el cociente entre el cateto adyacente al ángulo y la hipotenusa del triángulo:
Ejemplos de cálculo de la hipotenusa
Aquí compartimos cuatro casos en los que calculamos la hipotenusa, sirviéndonos del Teorema de Pitágoras y las razones trigonométricas.
Ejemplo 1 con catetos conocidos
Imaginemos que tenemos un triángulo rectángulo con un cateto que mide 9 centímetros, y el otro, 12 centímetros:
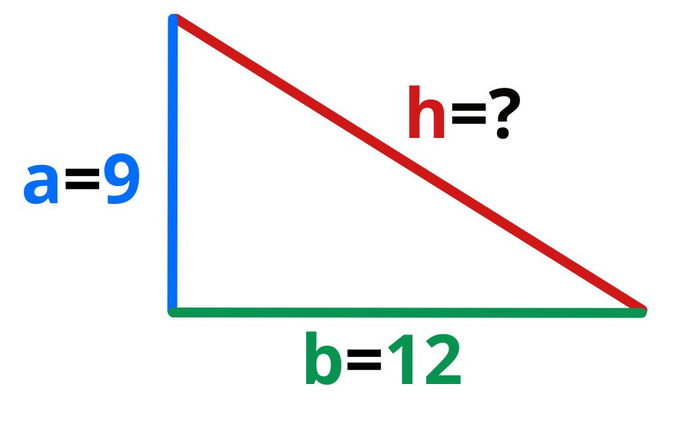
Como conocemos el valor de los dos catetos, podemos emplear el Teorema de Pitágoras. Resolvamos la ecuación:
Por lo tanto, la hipotenusa mide 15 centímetros.
Ejemplo 2 con catetos conocidos
Pongamos el caso de un triángulo rectángulo que contiene un cateto que mide 5,2 metros y otro de 3,6 metros:
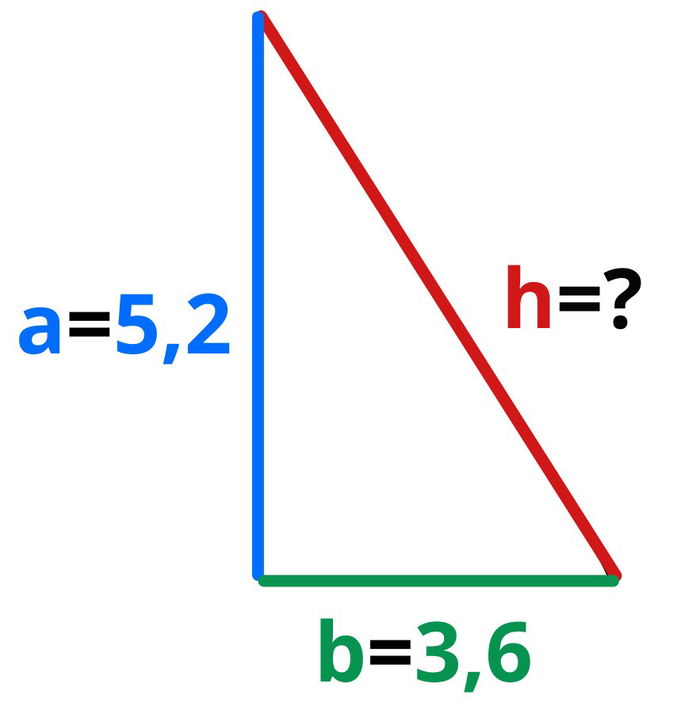
Los dos catetos son conocidos, así que apliquemos el Teorema de Pitágoras:
En este caso, tenemos un resultado con infinitas cifras decimales. Como los catetos solo presentan una cifra decimal, podemos redondear el resultado a una cifra decimal, o sea, 6,3 metros, aunque eso dependerá del grado de exactitud que deseemos.
Ejemplo 3 con el seno y coseno
Ahora imaginemos un triángulo en el que solo conocemos el valor de uno de los catetos, pero también cuánto miden todos los ángulos:
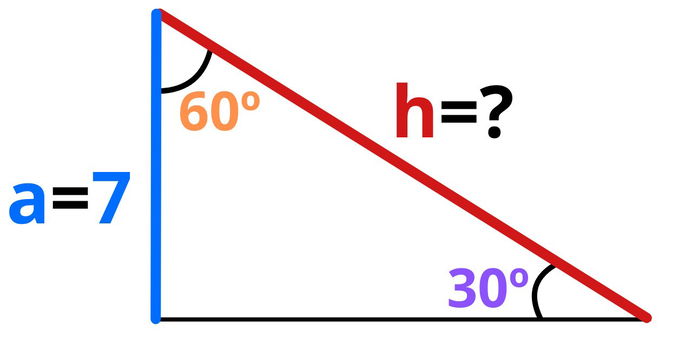
A partir de estos datos, podemos calcular la hipotenusa a través de las razones trigonométricas seno y coseno. Si optamos por el seno, hemos de tomar el ángulo de 30º:
Por otro lado, también podemos obtener la hipotenusa con el coseno, pero debemos usar el ángulo de 60º:
Ten en cuenta que, si haces estos cálculos con la calculadora, asegúrate de que esté en modo grados o DEG, y no en radianes o RAD. De lo contrario, tendrás que pasar los grados del ángulo a radianes.
Vea también Razones trigonométricas y Triángulo rectángulo.
Cómo citar: Significados, Equipo (29/02/2024). "Hipotenusa". En: Significados.com. Disponible en: https://www.significados.com/hipotenusa/ Consultado: