Fracción
Una fracción es la representación de las partes de un todo, es decir, se divide en partes iguales en las que cada una es una fracción del entero.

Por ejemplo: dividimos una pizza en 8 trozos iguales, por lo que cada pedazo corresponde a un 1/8 (un octavo) del total. Si un individuo come seis pedazos, podemos decir que comió 6/8 (siete octavo) de la pizza, y quedaría 2/8 (dos octavo).
Las fracciones, o números fraccionarios, son parte de los números racionales, y se suelen utilizar para representar números diferentes a los enteros. De hecho, una fracción es una división entre dos números enteros, de la cual resulta en otro número que puede contener una o varias cifras decimales.
Tomemos la siguiente fracción como ejemplo:
Si realizamos la división, obtenemos como resultado el número decimal 0,5. Tanto la fracción como el número decimal son la misma cantidad, por lo que ambas formas se pueden utilizar para representar un mismo valor. No obstante, las fracciones nos permiten realizar operaciones aritméticas sin tener que manejar decimales.
Las fracciones se componen de dos partes: un término superior, llamado numerador o dividendo, y un término inferior, conocido como denominador o divisor. Ambos están separados por una barra oblicua u horizontal, un símbolo utilizado para indicar una división entre términos.
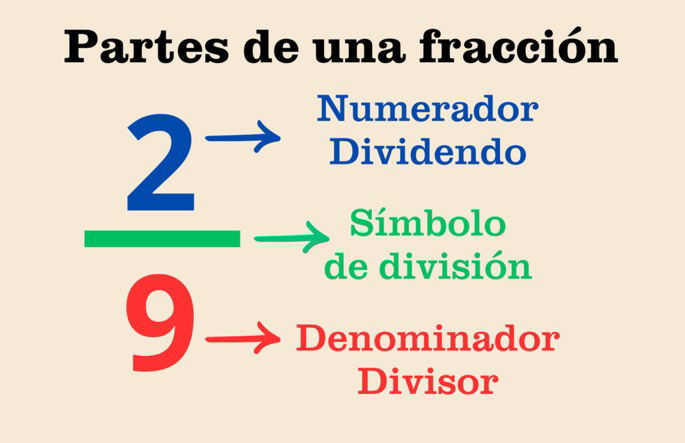
Por ejemplo, en la siguiente fracción:
El número 2 es el término superior de la fracción; por lo tanto, se trata del numerador o dividendo. En cambio, el número 9 es el término inferior de la fracción, es decir, es el denominador o divisor.
Ten en cuenta que el valor del numerador puede ser menor, mayor o igual que el del denominador. Dependiendo de la relación de proporción entre ambos, hablamos de un tipo de fracción u otro.
Tipos de fracciones y ejemplos
Existen diferentes tipos de fracciones, como las propias, impropias y mixtas, además de reducibles e irreducibles, entre otros. Los comentamos a continuación.
Fracción propia
Una fracción propia es aquella en el que el valor del numerador, es decir, el término superior, es menor que el del denominador, o sea, el término inferior. Por lo tanto, se cumple lo siguiente: numerador < denominador.
Veamos el siguiente ejemplo:
En esta fracción, el numerador tiene un valor de 2, mientras que el denominador es 7. Como 2 es menor que 7, estamos ante una fracción propia.
Fracción impropia
Una fracción impropia es aquella en el que el valor del numerador, es decir, el término superior, es mayor o igual que el del denominador, o sea, el término inferior. En este caso, se cumple lo siguiente: numerador ≥ denominador.
Por ejemplo:
A diferencia del ejemplo de la fracción propia, aquí el numerador y denominador son 7 y 2, respectivamente. Como 7 es mayor que 2, se trata de una fracción impropia.
Otro ejemplo sería:
Como el numerador y el denominador de la fracción coinciden, también se trata de una fracción impropia.
Fracción mixta
Una fracción mixta es la combinación de un número entero y una fracción propia que se suman entre sí. Veamos el siguiente ejemplo:
La parte entera de esta fracción mixta es 2, mientras que la fracción propia se compone de 4 como numerador y 6 como denominador. Estos dos términos se pueden sumar, ya que el número entero de esta fracción mixta, 2 en este caso, es en realidad una fracción impropia.
Lo que nos indica el número entero es cuántas veces se ha completado la unidad de la fracción propia a la que acompaña (4/6). En el ejemplo que nos ocupa, el valor 2 es equivalente a:
Si sustituimos y sumamos, a partir de la fracción mixta obtendremos una fracción impropia:
Por lo tanto, se puede decir que una fracción mixta es aquella fracción impropia que se ha desglosado en un número entero y una fracción propia.
Otros tipos de fracciones
Fracción reducible
Una fracción reducible es aquella que se puede simplificar, ya que el numerador y el denominador tienen divisores comunes mayores a 1 que hacen posible reducirla sin emplear cifras decimales.
Por ejemplo:
Los valores 9 y 15 tienen un divisor común, que es 3. Si dividimos ambos por esa cifra, obtenemos la siguiente fracción:
Es decir, 3/5 es la fracción reducida de la fracción reducible 9/15.
Fracción irreducible
A diferencia de la reducible, la fracción irreducible es aquella cuyo numerador y denominador no poseen divisores comunes mayores a 1. Por lo tanto, no podemos dividir ambos por un número entero sin que nos dé cifras decimales en el numerador o denominador.
Por ejemplo:
El numerador, 5, tiene dos divisores: 1 y 5. El denominador, en cambio, tiene tres divisores: 1, 3 y 9. El único divisor común entre ambos elementos de la fracción es 1; por esa razón, esta fracción es irreducible.
Otros ejemplos de fracciones irreducibles son:
Fracción decimal
La fracción decimal es aquella que tiene como denominador un múltiplo de 10. Algunos ejemplos son los siguientes:
Fracciones equivalentes
Se da cuando dos fracciones tienen el mismo valor decimal. En otras palabras, se multiplica o divide el numerador y denominador por el mismo número y la fracción mantiene su valor.
Por ejemplo, las dos siguientes fracciones son equivalentes:
Podemos comprobarlo mediante el método de la fracción reducible, es decir, hallando divisores comunes. En este caso, 4 y 8 tienen dos divisores comunes: 2 y 4. Si dividimos ambos por 2, obtenemos:
Operaciones con fracciones
Suma y resta de fracciones
Si dos fracciones tienen un denominador común, realizar una suma o resta es bien sencillo, pues solo hemos de sumar o restar los numeradores. Miremos los siguientes ejemplos:
Ahora bien, para sumar o restar dos fracciones con denominadores diferentes, primero debemos multiplicar en cruz los numeradores con los denominadores. Es decir, multiplicamos el numerador de la primera fracción por el denominador de la segunda fracción, y luego el denominador de la primera fracción por el numerador de la segunda fracción.
Veamos este ejemplo:
Acto seguido, como se trata de una suma de fracciones, sumamos los resultados para obtener el numerador de esta operación:
Después debemos multiplicar los dos denominadores entre sí, 4 y 3, para obtener un denominador común en esta operación:
El resultado de la suma de fracciones con diferente denominador es el siguiente:
Multiplicación y división de fracciones
La multiplicación entre dos fracciones se hace siempre de la misma forma, aunque los denominadores de las fracciones no coincidan. Para realizar esta operación, multiplicamos los numeradores entre sí, y de igual manera se multiplican los denominadores entre sí.
Por ejemplo:
Como has podido ver, la fracción final resulta de multiplicar los dos numeradores, 3 y 7, y los dos denominadores, 4 y 9, por separado.
La división sigue un proceso distinto. En este caso, hemos de multiplicar el numerador de la primera fracción por el denominador de la segunda; de aquí resulta el numerador de la fracción final. A continuación, se multiplica el denominador de la primera fracción por el numerador de la segunda; de aquí resulta el denominador de la fracción final.
Veamos el siguiente ejemplo:
Para hallar el numerador de esta división de fracciones, multiplicamos el numerador de la primera fracción por el denominador de la segunda:
Seguidamente, multiplicamos el denominador de la primera fracción por el numerador de la segunda fracción para hallar el denominador resultante:
Por lo tanto, el resultado de la división de estas fracciones es:
Ver también:
Cómo citar: Significados, Equipo (27/02/2025). "Fracción". En: Significados.com. Disponible en: https://www.significados.com/fraccion/ Consultado: