Estadística
La estadística es la ciencia encargada de estudiar los datos. Esta incluye recolectar, analizar y describir los datos para llegar a conclusiones sobre un fenómeno en particular.
La estadística emplea herramientas matemáticas y de probabilidades, con las cuales desarrolla métodos y modelos para analizar los datos. Estos métodos estadísticos se aplican en diversas áreas de las ciencias naturales y sociales, la publicidad y el mercadeo, el sector industrial y el entretenimiento.

Un análisis estadístico sirve para comprender un hecho, realizar un estudio de mercado, hallar la raíz a problemas sociales, comprender el comportamiento de una población, etc.
La estadística ofrece una variedad de aplicaciones útiles en distintos escenarios, como:
- Identificar los productos más vendidos en una tienda.
- Realizar pronósticos del tiempo basados en datos climáticos.
- Analizar el desempeño de los equipos deportivos. Esto incluye partidos ganados, perdidos y empatados, información que resulta útil para predecir resultados en distintos juegos.
- Ayudar a los gobiernos a conocer las características de su población y economía, lo que les permite tomar decisiones informadas basadas en datos reales.
- Permitir a las empresas conocer a sus competidores y mejorar su rendimiento en el mercado.
- Servir como base indispensable para los investigadores científicos, quienes analizan los datos y sacan conclusiones a partir de ellos.
La estadística ha estado presente durante milenios. Civilizaciones como la egipcia o la Antigua Grecia realizaban censos para entender la distribución de la población y la posesión de tierras, por ejemplos. Eso sí, no fue hasta el siglo XVIII en que el término de estadística se creó y se popularizó gracias a Gottfried Achenwall y John Sinclair.
Tipos de estadística y ejemplos
A continuación se presentan los principales tipos de estadísticas aplicadas en diversos estudios: la descriptiva y la inferencial.
Estadística descriptiva
La estadística descriptiva o deductiva permite presentar de manera resumida y organizada los resultados obtenidos tras un estudio o análisis en particular. Su objetivo es describir las características principales de los datos reunidos.
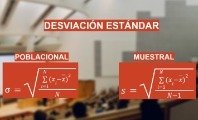
En la estadística descriptiva encuentras el promedio, la desviación estándar, la frecuencia, los porcentajes, cómo están distribuidos los datos, entre otros parámetros.
Ejemplo de estadística descriptiva
En un equipo de futbol se obtuvieron los siguientes datos:
| Identificación | Altura (en metros) | Edad | Goles en el último Mundial |
|---|---|---|---|
| 1 | 1.65 | 36 | 0 |
| 2 | 1.80 | 30 | 0 |
| 3 | 1.70 | 24 | 0 |
| 4 | 1.60 | 24 | 0 |
| 5 | 1.85 | 25 | 0 |
| 6 | 1.75 | 31 | 1 |
| 7 | 1.68 | 21 | 1 |
| 8 | 1.72 | 28 | 4 |
| 9 | 1.70 | 35 | 7 |
| 10 | 1.73 | 29 | 0 |
| 11 | 1.78 | 22 | 0 |
El promedio de altura de los jugadores de este equipo es de 1,724 metros con una desviación estándar de 0,070, el promedio de edad es de 27,72 años y el promedio de goles es 1,18.
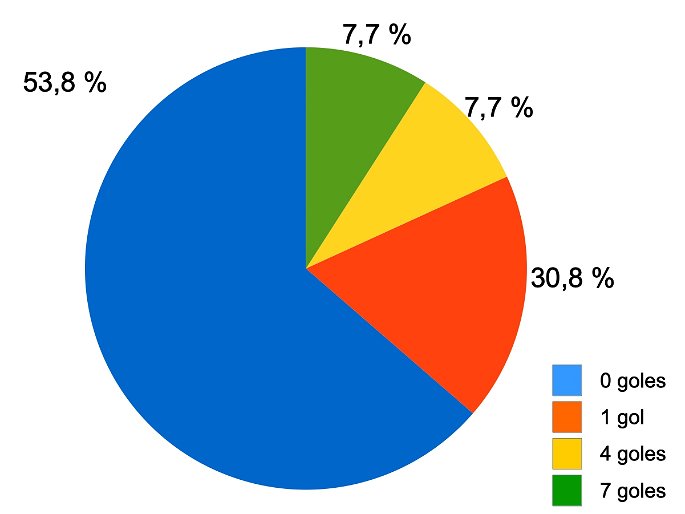
Con respecto a los goles anotados en el último mundial, el 53,8 % de los jugadores no anotó ningún gol; el 30,8 % anotó un gol; el 7,7 % anotó 4 goles; y otro 7,7 % anotó 7 goles.
Vea también Estadística descriptiva.
Estadística inferencial
La estadística inferencial o inductiva utiliza técnicas a partir de las cuales se obtienen generalizaciones, modelos o predicciones. También sirve para tomar decisiones basándose en información parcial o completa, obtenida mediante la estadística descriptiva.
Por lo general, se aplica estadística inferencial cuando se hacen estudios de medicamentos o se comparan grupos diferentes.
Ejemplo de estadística inferencial
Supongamos que se realiza un estudio en 100 pacientes con niveles de colesterol en sangre alto. 50 reciben un placebo y 50 reciben un medicamento. Se miden los niveles de colesterol luego de 8 semanas, y se obtienen los siguientes resultados:
- Grupo control (placebo): media de 250 mg/dL y desviación estándar de 25 mg/dL
- Grupo tratamiento (medicamento): media de 200 mg/dL y desviación estándar de 30 mg/dL
Para determinar si el nuevo tratamiento es eficaz, se aplican pruebas específicas, como la t de Student. En este caso, la diferencia entre el grupo control y el grupo de tratamiento es estadísticamente significativa, lo que quiere decir que el nuevo tratamiento tuvo un efecto.
Vea también Muestra.
Conceptos principales en estadística
La estadística emplea sus propios términos para describir y analizar los datos. Veamos algunos de los más importantes.
Datos:son los valores observados de las variables. También pueden llamarse como frecuencias.
Unidades muestrales: son los objetos de interés de un estudio. Las unidades muestrales pueden ser tornillos, personas o latas de frijoles como individuos, o pueden ser unidades compuestas por muchos individuos, como ciudades, escuelas o lotes de tornillos.
Población en estudio: es el conjunto completo de unidades muestrales que interesa estudiar con el fin de responder una pregunta de investigación. Por ejemplo, si estamos estudiando las orquídeas de una reserva natural, todas las orquídeas corresponden a la población en estudio.
Muestra de la población: cuando se quiere estudiar una población, pero es difícil poder acceder a todos los integrantes de la misma. Por ello, se toma una muestra, es decir, una porción o un subgrupo de la población.
Por ejemplo, en la ciudad de Monterrey hay más de 5 millones de habitantes. Si queremos estimar la altura de los adolescentes entre 14 y 16 años de la ciudad de Monterrey, tenemos que recurrir a una muestra de esta población, probablemente entre 100 y 500 personas.
Parámetro: es el valor que describe una población.
Estadístico: es el valor que se obtiene a partir de una muestra.
Error de estimación: es la diferencia entre el estadístico de la muestra y el parámetro de la población.
Margen de error: mide la diferencia máxima que se espera tener entre un resultado obtenido a partir de una muestra y su valor poblacional verdadero. Se acostumbra a tener un margen de error del 5 %, 2,5 % o 1 %.
Muestreo: es la forma en que se seleccionan las unidades muestrales para un estudio poblacional. El muestreo puede ser aleatorio simple, donde todos los individuos tiene la misma oportunidad de ser escogidos, o muestreo sesgado cuando se escogen cierto tipo de individuos.
Muestreo sistemático: comienza con una unidad elegida al azar y a partir de allí se toma una unidad cada cierto número fijo.
Por ejemplo, se quiere hacer un estudio de control de calidad en una fábrica de salsa de tomate. Se escoge un frasco de salsa de tomate cada 50 frascos en un lote de 5000. A estos 100 frascos se les hace las pruebas necesarias para asegurar que el lote tiene las condiciones adecuadas para salir a la venta.
Muestreo aleatorio estratificado: la población se divide en grupos homogéneos llamados estratos, y de cada estrato se hace un muestreo aleatorio simple.
Por ejemplo, en una ciudad la población se podría estratificar por menores de 10 años, entre 11 y 20 años, entre 21 y 30 años y mayor de 31 años.
Muestra representativa: una buena muestra debe ser representativa de la población. Esto significa, que todas las características importantes de la población tienen que estar en la muestra en la misma proporción que en la población.
Promedio: es el valor característico o central de un conjunto de números. Dentro de estos valores podemos hablar de la media (se obtiene sumando todos los valores del conjunto de datos y dividiendo la suma por la cantidad de datos en ese conjunto) y la mediana (el valor central de conjunto de datos ordenados).
Desviación estándar: es una medida de dispersión basada en la media. Representa una distancia típica de cualquier punto del conjunto de datos a su centro (medido por la media).
Intervalos de confianza (IC): se refiere a un rango de valores posibles y con un cierto porcentaje donde se puede asegurar que se encuentra el verdadero valor de un parámetro de la población.
Por ejemplo, si el intervalo de confianza al 95% de la altura de una población es (165,175) quiere decir que si repetimos las mediciones el 95% de las veces caerá entre los valores de 165 y 175.
Variables: son características que pueden cambiar de una unidad muestral a otra. Existen variables numéricas (o cuantitativas) y variables categóricas (o cualitativos).
Por ejemplo, en la siguiente tabla se muestran las variables de 10 perros que fueron llevados a consulta en un veterinario. Las variables sexo, raza y presencia de enfermedades son variables categóricas, mientras que la edad y el peso son variables numéricas.
| Sexo (Variable categórica) |
Meses de edad |
Raza (Variable categórica) |
Peso (en kg) (Variable numérica) |
Presencia de enfermedades (Variable categórica) |
|---|---|---|---|---|
| Macho | 12 | Labrador Retriever | 20 | No |
| Hembra | 24 | Bulldog | 15 | Sí (leishmaniasis) |
| Macho | 8 | Pastor Alemán | 30 | No |
| Hembra | 36 | Chihuahua | 2 | Sí (Dermatitis) |
| Macho | 7 | Golden Retriever | 25 | No |
| Hembra | 48 | Boston Terrier | 10 | No |
| Macho | 2 | Bóxer | 28 | Sí (obesidad) |
| Hembra | 16 | Dálmata | 20 | No |
| Macho | 60 | Rottweiler | 35 | Sí (displasia de cadera) |
| Hembra | 2 | Caniche | 6 | No |
Ver también:
Referencias
Kelmansky, D.M. (2009) Estadística para todos, Estrategias de pensamiento y herramientas para la solución de problemas. Instituto Nacional de Educación Tecnológica, Ministerio de Educación de Argentina.
Rumsey, D.(2010) Statistics Essentials for Dummies. Wiley publishing. Indiana
Cómo citar: Significados, Equipo (06/01/2025). "Estadística". En: Significados.com. Disponible en: https://www.significados.com/estadistica/ Consultado: