Ejemplos de estadística descriptiva para entender los conceptos básicos
La estadística descriptiva es una rama de la estadística que se encarga de describir un conjunto de datos a través de números, lo que ayuda a resumirlos y facilita su comprensión. Esto nos permite visualizar cómo están distribuidos los datos, los valores más frecuentes y los valores centrales.
Algunos ejemplos de estadística descriptiva serían la media de la edad, el porcentaje de género y el histograma de distribución de la edad de una población.
La estadística descriptiva se diferencia de la estadística inferencial. La primera ofrece información sobre un conjunto de datos completo, mientras que la segunda ofrece conclusiones generales a partir de una muestra de toda una población.
La estadística descriptiva se aplica en diversas áreas, desde la ciencia, el mercadeo, el entretenimiento y la industria en general.
Conceptos básicos en la estadística descriptiva
Datos cualitativos y cuantitativos
Los principales tipos de datos estadísticos son los cualitativos o categóricos y los cuantitativos o numéricos.
Los datos cualitativos representan aspectos de un individuo como el color del cabello, la nacionalidad, la religión, la marca de teléfono móvil que usa, el sabor preferido de helado o el tipo de flor que más le gusta, entre otros. Estos datos se caracterizan porque no pueden ser expresados por números.
Los datos cualitativos sirven para clasificar a los individuos en grupos. Por ejemplo, si en una comunidad de 1000 personas hay 20 argentinos, 25 venezolanos, 300 guatemaltecos y el resto son mexicanos, podemos calcular el porcentaje que representa cada nacionalidad.
En cambio, los datos cuantitativos son características que pueden expresarse en números o cantidades, como el número de horas trabajadas en una semana, la cantidad de pasos que se camina en un día, la cantidad de personas que asisten a una obra de teatro o el tiempo que se invierte navegando en Internet.
Media o promedio estadístico
La media o promedio es el valor medio de todos los datos que integran una muestra. Se representa con una X (equis) con una barra horizontal por arriba (x̄) cuando se refiere a una muestra y µ (letra griega mu) cuando se refiere a una población. Se aplica únicamente a los datos numéricos.
La media es una medida de centralidad de la estadística descriptiva. Se calcula sumando todos los valores y luego dividiéndolos por la cantidad de datos.
Por ejemplo, si estos son los datos del peso en gramos de 10 manzanas: 225, 230, 242, 233, 267, 212, 222, 290, 233, 236.
El promedio será 239 gramos.
Mediana
Otra variable estadística que se usa para determinar un valor central es la mediana. La mediana es el valor en la mitad cuando los datos se arreglan de menor a mayor.
Por ejemplo, en las 10 manzanas del ejemplo anterior, ordenamos los valores de menor a mayor:
- 212
- 222
- 225
- 230
- 233
- 233
- 236
- 242
- 267
- 290
Para un número par de datos, se toman los dos datos centrales (en este caso el 5 y el 6) y se promedian. En nuestro caso tenemos los valores 233 y 233, por lo que la mediana será 233.
Para un número impar de datos, se toma el dato de la mitad. Si tenemos 11 datos, el valor del dato 5 será la mediana.
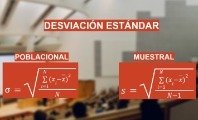
Desviación estándar
La desviación estándar es la medida de variabilidad más ampliamente empleada. Representa la distancia desde cualquier dato hasta el centro y se denota la por la letra s minúscula.
La desviación estándar es útil para determinar la dispersión y variación de los datos. Por ejemplo, en estos dos grupos de datos:
- 0, 200, 400
- 199, 200, 201
El promedio y la mediana es el mismo en ambos casos, pero nos podemos dar cuenta que ambos conjuntos de datos tienen una dispersión muy diferente. En el primer caso, la desviación estándar es 200, mientras en el segundo caso es 1.
Mientras más pequeña es la desviación estándar, más cercanos se encuentran los datos.
Percentiles
Un percentil es el número de individuos que en los registros de datos se encuentran por debajo del valor solicitado. Por ejemplo, si un bebé está en el percentil 90 de peso, significa que el 90 por ciento de los bebés está por debajo del peso de este bebé.
Un percentil no es un porcentaje, sino un número que representa un dado porcentaje de los datos ordenados de menor a mayor. Por ejemplo, estos son las notas de un examen de matemática del 1 al 100:
20, 40, 45, 46, 48, 50, 51, 52, 53, 54, 60, 70, 80, 90, 92, 93, 94, 95, 96, 99
Queremos saber en qué percentil se encuentra la persona que sacó 80 en el examen. Para esto contamos los datos por debajo de 80, que es igual a 13. Entonces hacemos el siguiente cálculo:
Esto significa que 65 por ciento de los valores están por debajo del dato 80.
Histograma
El histograma es un tipo de gráfico de barras aplicado a los datos numéricos. Sirve para visualizar cómo están distribuidos los datos, por ejemplo, si son simétricos, en forma de campana, con tendencia hacia el lado izquierdo o derecho.
En el ejemplo siguiente, se graficaron las calificaciones de un examen de matemáticas del tercer año de un salón con 30 estudiantes. El eje horizontal representa las calificaciones, mientras en el eje vertical se presenta la frecuencia o el número de veces que se repite un dato. En este caso, 8 personas sacaron 15 de calificación.
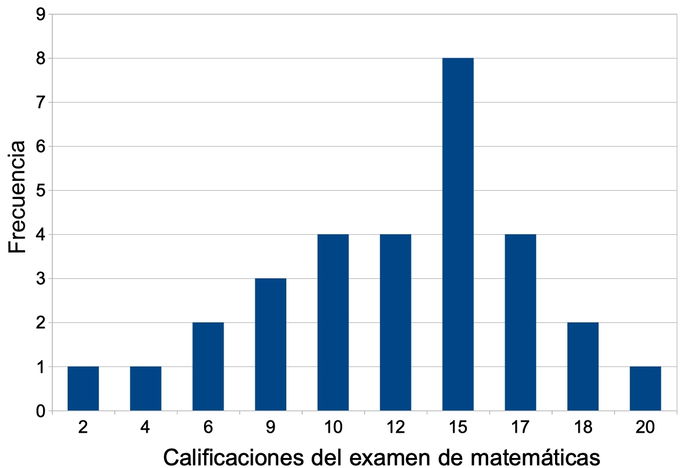
Histograma de calificaciones de un examen obtenidas por 30 estudiantes.
Moda
La moda es el valor que más aparece en un conjunto de datos. Se considera también una medida de la tendencia central.
En el ejemplo anterior, la moda es 15, la calificación que más se repite en este examen con 8.
Vea también:
Referencias
Rumsey, D. (2010) Statistics Essentials for Dummies. Wiley Publishing. NJ.
Salazar P., C., Del Castillo G., S. (2018) Fundamentos Básicos de Estadística, Primera edición.
Cómo citar: (15/09/2023). "Ejemplos de estadística descriptiva para entender los conceptos básicos". En: Significados.com. Disponible en: https://www.significados.com/estadistica-descriptiva/ Consultado: