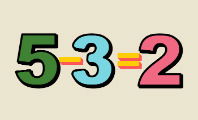División (matemáticas)

Revisado por Rafael C. Asth

Profesor de Matemática y Física

La división es una de las operaciones básicas de la aritmética y consiste en separar en partes iguales un total. Es decir, si tenemos una cantidad y queremos dividirla en partes iguales, podemos utilizar la división para determinar cuántas partes iguales obtenemos y qué cantidad corresponde a cada parte.

Por ejemplo, si tenemos 10 unidades y queremos dividirlas en 5 partes iguales, corresponderán 2 unidades a cada parte.

105 = 2

El símbolo de la división es el signo (÷), aunque también puede representarse mediante dos puntos (:) o una barra oblicua (/). Se coloca entre los números que participan en la operación, el dividendo o parte total y el divisor o número de partes iguales que se quiere separar.

La división es la operación contraria a la multiplicación. Por lo tanto, para saber si una división es correcta, se puede multiplicar el resultado, también llamado cociente, por el divisor. Por ejemplo:

10 ÷ 5 = 2, por lo tanto, 2 x 5 = 10, la división es correcta.

Partes de la división

Una división está formada por cuatro elementos:

• Dividendo: es la cantidad total que se quiere repartir en partes iguales.

• Divisor: es la cantidad de partes en la que se va a dividir el dividendo.

• Cociente: es el resultado de la división. En otras palabras, es el número de veces que el divisor “cabe” en el dividendo.

• Resto: es la cantidad que queda sobrante después de realizar una división cuyo resultado no es exacto.

Por ejemplo, si dividiéramos 10 ÷ 3 obtendríamos un cociente de 3 y un resto de 1.

Ver también: Multiplicación, Suma y Resta (matemáticas)

Cómo realizar una división

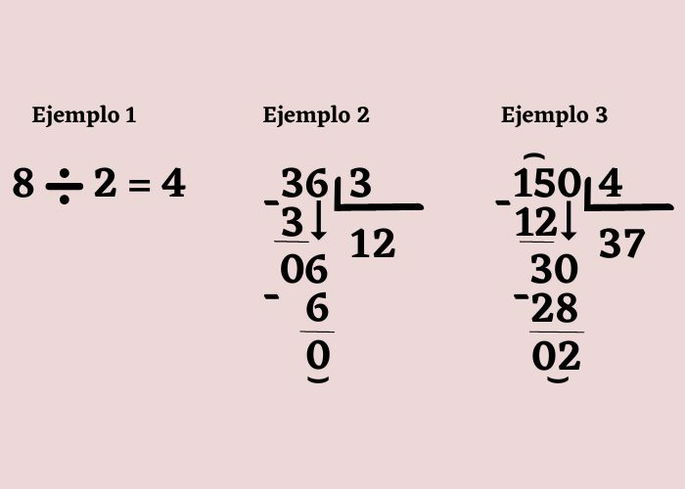
1. Colocamos a la izquierda el dividendo y a la derecha el divisor, separados por el símbolo de la división. Por ejemplo, 8 ÷ 4 = 2. Para resolver divisiones de una cifra debemos buscar el número que multiplicado por el divisor de como resultado el dividendo (4 x 2 = 8). (Ver ejemplo 1).
2. En divisiones largas podemos utilizar el ángulo para diferenciar los factores de la división (ver ejemplo 2). Comenzamos por la primera cifra del dividendo. Buscamos un número que, multiplicado por el divisor, dé como resultado dicho número o el que más se aproxime sin pasarse. Anotamos el resultado de la multiplicación debajo de la primera cifra del dividendo y restamos ambos números, separando la diferencia mediante una línea horizontal.
3. Anotamos el cociente de la operación bajo el ángulo.
4. Continuamos bajando la segunda cifra de dividendo junto a la diferencia de la resta del paso 2. Volvemos a buscar el número que, multiplicado por el divisor, dé como resultado dicha cifra o la más aproximada. Colocamos el resultado de la multiplicación bajo la segunda cifra del dividendo, restamos y anotamos la diferencia, separada con una línea horizontal.
5. Anotamos nuevamente el cociente de la operación bajo el ángulo y cerramos la operación marcando el resto con una línea curva.
6. Cuando la primera cifra del dividendo es menor que el divisor, tomaremos también la cifra siguiente, como vemos en el ejemplo 3.

Vea también:

• Aritmética
• División con decimales
• Ley de los Signos

Cómo citar: Significados, Equipo (09/09/2024). "División (matemáticas)". En: Significados.com. Disponible en: https://www.significados.com/division/ Consultado: