Cuadrilátero
Un cuadrilátero, en geometría, es un polígono que cuenta con cuatro ángulos y cuatro lados. Los cuadriláteros pueden presentar diversas formas, pero todos cumplen con estas características: cuatro vértices, cuatro lados, dos diagonales y la propiedad de que la suma de sus ángulos internos siempre es 360°.
Además, todos los cuadriláteros también pueden llamarse cuadrángulos, ya que tienen cuatro ángulos.
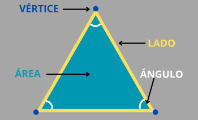
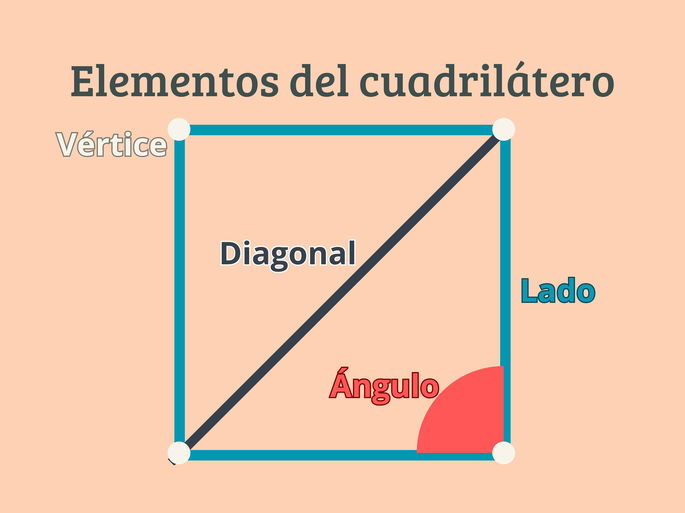
Características y elementos del cuadrilátero
Cuatro lados, todos los cuadriláteros tienen cuatro lados unidos por los vértices contiguos.
Cuatro vértices o puntos de intersección de los lados que lo conforman.
Dos diagonales, que son segmentos de línea que unen vértices no contiguos.
Cuatro ángulos internos, formados por dos lados contiguos, cuya suma siempre es 360°
Cuatro ángulos exteriores, que son determinados por la prolongación de cada uno de los lados sobre un vértice.
Propiedades de los cuadriláteros
Lados paralelos: dependiendo del tipo, algunos cuadriláteros pueden tener pares de lados paralelos.
- Los paralelogramos tienen dos pares de lados paralelos (ej., cuadrados, rectángulos, rombos).
- Los trapecios tienen solo un par de lados paralelos.
- Los trapezoides no tienen lados paralelos.
Diagonales:
- En paralelogramos, las diagonales se bisecan entre sí. Cada diagonal corta a la otra en dos segmentos iguales, creando un punto de intersección que es el centro del paralelogramo.
- En cuadrados y rectángulos, las diagonales son de igual longitud. En estos tipos de paralelogramos, además de bisecarse, las diagonales miden lo mismo. Esto se debe a que los cuadrados y rectángulos tienen ángulos internos de 90°, lo cual los hace figuras simétricas.
- En un rombo, las diagonales son perpendiculares entre sí, se bisecan en su punto de intersección, pero formando un ángulo de 90°. Esta propiedad de perpendicularidad permite dividir el rombo en cuatro triángulos rectángulos de igual área.
Ángulos interiores y exteriores:
- En cuadriláteros convexos (cuyos vértices están en el exterior), todos los ángulos interiores son menores a 180°.
- En cuadriláteros cóncavos (los que tienen al menos un vértice apuntando hacia el interior del polígono), al menos uno de los ángulos interiores es mayor a 180°.
Simetría:
- Los cuadrados y rectángulos tienen simetría axial (tiene cuatro ejes de simetría que dan lugar a mitades que coinciden perfectamente) y de rotación (implica que si rotamos el cuadrado menos de 360º, podemos hallar formas idénticas).
- Los rombos tienen simetría axial, tienen dos ejes de simetría, que son sus diagonales. Al doblarlo sobre cualquiera de las diagonales, ambas mitades coinciden.
- Otros cuadriláteros, como los trapezoides asimétricos y otros cuadriláteros irregulares, carecen de simetría, no tienen ningún eje de simetría ni simetría de rotación.
Ver también: Figuras Geométricas y Polígono.
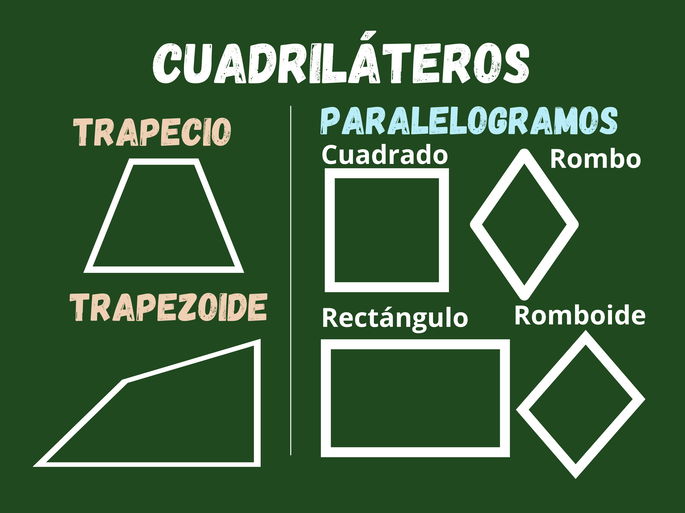
Tipos de cuadriláteros
Paralelogramo
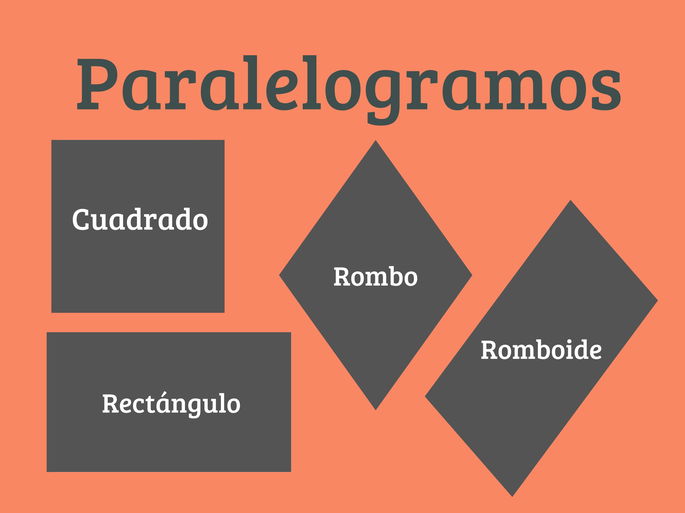
Un paralelogramo es un cuadrilátero con dos pares de lados opuestos que son paralelos entre sí. Los lados opuestos son de igual longitud, y los ángulos opuestos también son iguales.
Propiedades: las diagonales de un paralelogramo se bisecan, es decir, se dividen mutuamente en dos partes iguales en el punto donde se cruzan.
Ejemplos:
- Cuadrado: todos los lados son iguales y los cuatro ángulos son rectos (90°). Tiene simetría axial y de rotación.
- Rectángulo: los lados opuestos son iguales y todos los ángulos son rectos. Tiene simetría axial y de rotación, pero solo en ciertos ángulos.
- Rombo: todos los lados son iguales, pero los ángulos no necesariamente son de 90°. Las diagonales son perpendiculares y actúan como ejes de simetría.
- Romboide: los lados opuestos son iguales, pero los ángulos no son necesariamente de 90°. No tiene diagonales perpendiculares ni todos los lados iguales.
Ver también Cuadrado
Trapecio
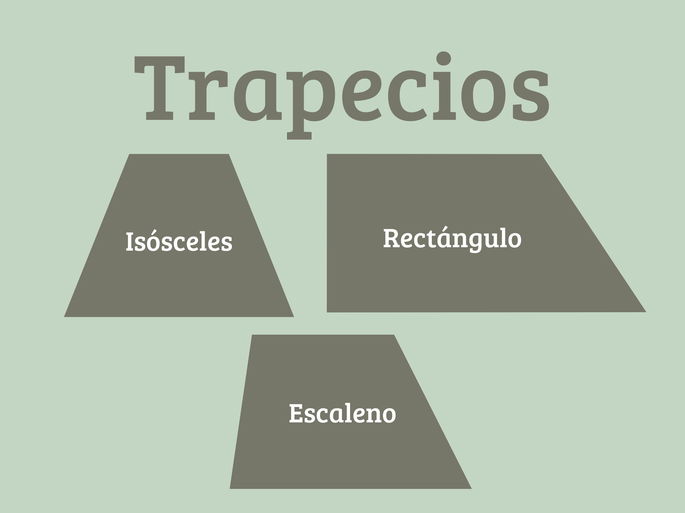
Un trapecio es un cuadrilátero con un solo par de lados paralelos. Los ángulos adyacentes a cada lado no son necesariamente iguales, lo que da lugar a diferentes tipos de trapecios.
Ejemplos:
- Trapecio isósceles: tiene un par de lados no paralelos de igual longitud, lo que le confiere un eje de simetría.
- Trapecio rectángulo: posee un ángulo recto (90°) en dos de sus vértices.
- Trapecio escaleno: no tiene lados de igual longitud, y todos sus ángulos son diferentes.
Trapezoide
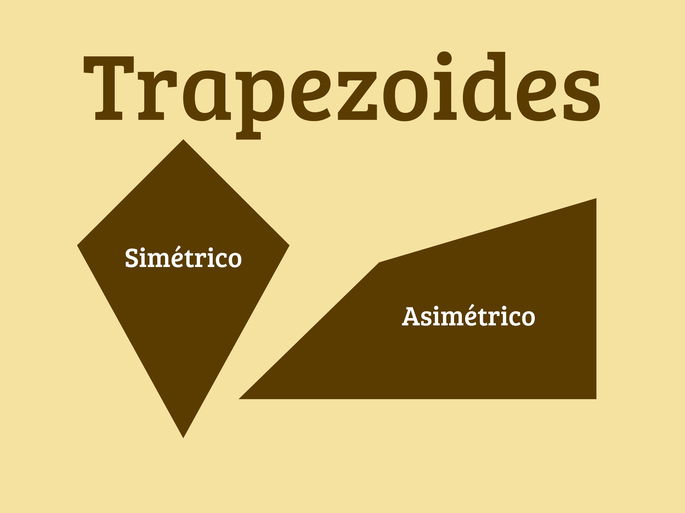
Un trapezoide es un cuadrilátero sin lados paralelos. Carece de simetría de rotación, no todos los lados son iguales, y no presenta una estructura específica de paralelismo entre sus lados, lo que le da una forma irregular.
Ejemplos:
- Trapezoide simétrico: aunque no tiene lados paralelos, puede tener cierta simetría axial y dos pares de lados iguales, especialmente en figuras como el cometa.
- Trapezoide asimétrico: no tiene lados paralelos ni simetría axial. Cada lado y cada ángulo puede ser de diferente medida.
Cuadriláteros cóncavos y convexos
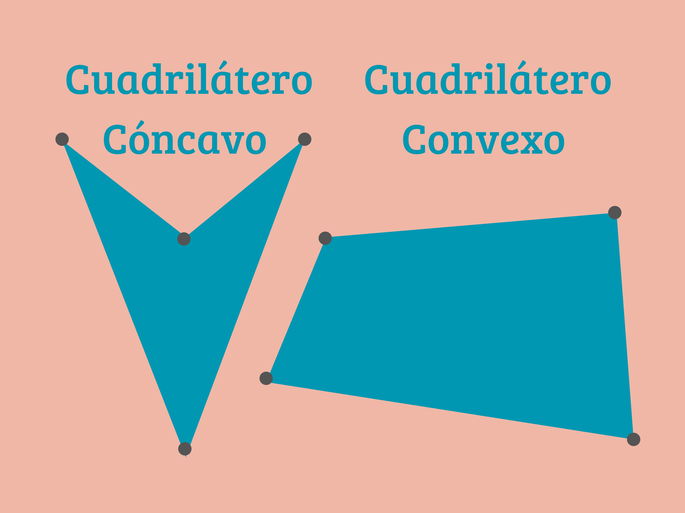
Cuadriláteros cóncavos
Son cuadriláteros que tienen al menos un ángulo interior mayor a 180° (ángulo reflejo).
Estos cuadriláteros presentan un hueco en uno de sus lados, lo cual les da una apariencia de estar doblados hacia adentro. Si trazamos una línea entre dos puntos en el interior de un cuadrilátero cóncavo, esta línea puede salir del área de la figura.
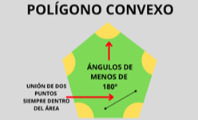
Cuadriláteros convexos
Todos sus ángulos interiores son menores a 180°, y ningún vértice entra o se dobla hacia adentro.
Si se elige cualquier par de puntos dentro del cuadrilátero, la línea que los conecta estará completamente dentro de la figura, ya que no presenta concavidades.
Ejemplos serían todos los tipos de paralelogramos, trapecios y trapezoides en los que los ángulos interiores son menores a 180°.
Vea también:
Referencias:
Pastor, A. J., Aguilera, F. C., & Rodríguez, A. G. (1992). Definiciones de triángulos y cuadriláteros: errores e inconsistencias en libros de texto de EGB. Revista Epsilon, 23, 49-61.
Bolt, B. (1998). ¿Qué es la geometría? Suma.
Cómo citar: Significados, Equipo (14/11/2024). "Cuadrilátero". En: Significados.com. Disponible en: https://www.significados.com/cuadrilatero/ Consultado:
