Círculo
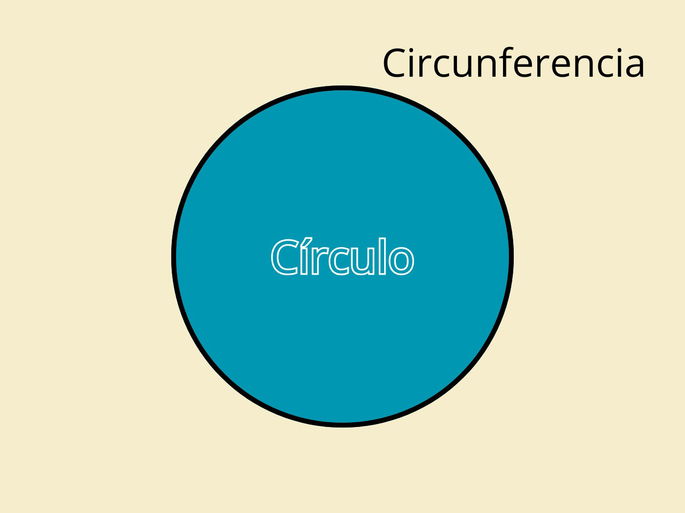
Un círculo es una figura geométrica plana y simétrica integrada por la superficie contenida dentro de una circunferencia. Es una de las figuras más importantes en la geometría debido a su perfecta simetría y sus numerosas propiedades.
El círculo se define como el conjunto de todos los puntos de un plano cuya distancia a un punto fijo (centro) es menor o igual que una variable constante (radio).
El círculo tiene varias características distintivas:
- Simetría: posee una simetría infinita en torno a su centro. Esto significa que puede girarse cualquier cantidad de grados alrededor de su centro sin cambiar su apariencia.
- Curva continua y cerrada: la circunferencia, o el perímetro del círculo, es una curva continua y cerrada sin esquinas ni bordes. Esto lo diferencia de figuras poligonales, como el cuadrado o el triángulo, que tienen lados rectos.
- Equidistancia: todos los puntos en la circunferencia están a la misma distancia del centro, lo que le otorga al círculo una perfecta simetría radial.
- Propiedad de área máxima: de todas las figuras planas con el mismo perímetro, el círculo es la que contiene el área máxima. Esta propiedad hace que el círculo sea óptimo para estructuras como contenedores o piezas de diseño que requieren aprovechar al máximo el espacio.
- Diámetros equivalentes: todos los diámetros de un círculo son iguales en longitud, ya que siempre representan el doble del radio y atraviesan el círculo de un lado al otro pasando por el centro.
En la vida cotidiana, los círculos se encuentran en numerosos objetos, desde relojes y monedas hasta ruedas y platos, ya que esta figura tiene propiedades útiles tanto en geometría como en física y otras ciencias aplicadas.
Ver también: Figuras Geométricas y Polígono
Partes del círculo
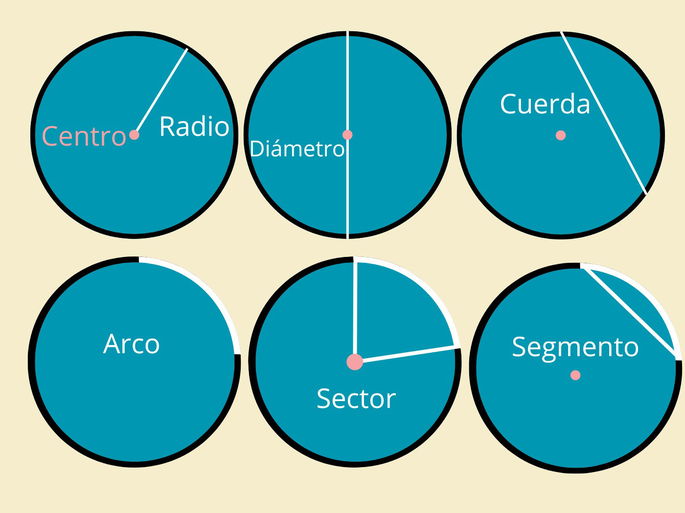
Estas son las partes del círculo esenciales para entender sus aplicaciones en geometría y cálculo.
Centro: es el punto interior equidistante de todos los puntos en la circunferencia. El centro es fundamental para definir la simetría del círculo.
Radio (r): segmento que une el centro del círculo con cualquier punto en la circunferencia. Todos los radios de un círculo tienen la misma longitud. Este valor es fundamental para calcular otras medidas como el área y la circunferencia.
Diámetro (d): es el segmento de línea que pasa por el centro y une dos puntos opuestos en la circunferencia. Es el doble de la longitud del radio (d = 2•r).
Circunferencia: es el borde o perímetro del círculo. Es la línea curva cerrada que forma el límite del círculo, y su longitud se calcula con C = 2•π•r.
Cuerda: es un segmento de línea que une dos puntos cualquiera de la circunferencia, sin necesariamente pasar por el centro. Cuando una cuerda pasa por el centro, se convierte en un diámetro, que es la cuerda más larga posible en el círculo.
Arco: es una porción o sección de la circunferencia comprendida entre dos puntos específicos. Un arco puede representar una pequeña curva o una mayor parte de la circunferencia, dependiendo de la distancia entre los puntos.
Sector circular: área delimitada por dos radios y el arco que conecta sus extremos. Se asemeja a una porción de pastel o pizza dentro del círculo.
Segmento circular: es la región del círculo comprendida entre una cuerda y el arco localizado entre los extremos de esa cuerda. Puede tener forma de luna o semicírculo si la cuerda coincide con el diámetro.
Propiedades del círculo
Área del círculo
El área de un círculo es la superficie que ocupa, el espacio contenido dentro de su circunferencia. Para hallarla, es común utilizar la siguiente fórmula: A = π•r², siendo π el número pi, utilizado en muchos casos como 3,1416 y r el radio de la circunferencia.
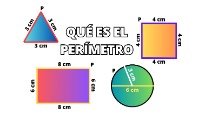
Perímetro del círculo
El perímetro de un círculo se corresponde con la circunferencia. Una de las propiedades más conocidas del círculo es que la relación entre la circunferencia y el diámetro es constante. Para calcular el perímetro se puede utilizar esta fórmula P = d•π, correspondiendo d al valor del diámetro de la circunferencia.
Proporcionalidad del círculo
El círculo posee unas propiedades de proporcionalidad con respecto al área, perímetro y radio. Por ejemplo, la circunferencia del círculo y el radio son directamente proporcionales, pues a mayor radio, más grande será la circunferencia. Asimismo, el área que comprende el círculo y el cuadrado del radio son también directamente proporcionales.
Tanto el área como el perímetro del círculo comparten una misma constante de proporcionalidad, que es el número pi (π).
Vea también:
Cómo citar: Significados, Equipo (11/11/2024). "Círculo". En: Significados.com. Disponible en: https://www.significados.com/circulo/ Consultado: